Many of the terms used in triangle geometry are presented in Eric Weisstein's MathWorld, including topics contributed by Darij Grinberg, Floor Lamoen, and Peter Moses.
A number of terms defined at MathWorld originated in this Glossary, using trilinear coordinates. The need for definitions using barycentric coordinates has led to P. L. Douillet's highly recommended Translation of Kimberling's Glossary into barycentrics, "Le Glossaire de Pierre"
In 2012, links to Tables were added to ETC. These tables include many examples of conjugates of various kinds (e.g., aleph, beth, gimel, he, waw, zayin, complementary, and anticomplementary), introduced in C. Kimberling, Collineations, Conjugacies, and Cubics, Forum Geometricorum 2 (2002) 21-32. Those definitions are included below.
In 2016, an Index of Triangles Referenced in ETC was provided by César Lozada. You can access it here, and also from Tables.
In this Glossary, points and lines are given in homogeneous coordinates. The coordinates are assumed to be trilinear unless otherwise indicated (as barycentric or polar coordinates), and they are used here to define points, lines, circles, triangle centers, etc. Likewise, zero determinants define collinearity and concurrence, etc. Consequently, triangle geometry is presented here at a much more general level than a single euclidean triangle. In this treatment, the symbols a,b,c are regarded as algebraic indeterminates or variables, so that points, as functions of a,b,c, are quite different from points in a two-dimensional plane. When (a,b,c) are real numbers restricted by the "triangle inequalities" for sidelengths (i.e., a ≤ b + c, b ≤ c + a, c ≤ a + b), the result is traditional triangle geometry. In favor of the greater generality, in this Glossary, algebraic definitions take precedence over traditional geometric construction-definitions. (For more in this vein, see the definitions of line, point, and symbolic substitution.)
The words "defined cyclically" apply after an "A-object" has been defined: if the A-object is F(A,B,C), then the B-object is F(B,C,A), obtained by the cyclic permutation ABC → BCA, and the C-object is, likewise, F(C,A,B). Example: If A' is the point where lines AP and BC meet, and B' and C' are defined cyclically, then B' is where lines BP and CA meet, and C' is where lines CP and AB meet.
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-aleph conjugate of U is the point
h(p,q,r,u,v,w) : h(q,r,p,v,w,u) : h(r,p,q,w,u,v),
where
h(p,q,r,u,v,w) = - q2r2u2 + r2p2v2 + p2q2w2 + (vw + wu + uv)( - q2r2 + r2p2 + p2q2).
Let g be the mapping given by
g(x : y : z) = -x/p + y/q + z/r : x/p - y/q + z/r : x/p + y/q - z/r.
The P-aleph conjugate of U is "what you do to g(X) to make g(X -1) when f(X) = U." (Hyacinthos #4111, Oct. 11, 2001.)
Let P be a point not on a sideline of ABC. Let A' = AP∩BC. Let A" be the harmonic conjugate of P with respect to A and A'. Define B" and C" cyclically. Triangle A"B"C" is the anticevian triangle of triangle ABC. (The lines AP, BP, CP are the cevians of P, and A'B'C', the cevian triangle of P.)
If P = p : q : r, then A" = - p : q : r, B" = p : - q : r, C" = p : q : - r.
Examples of anticevian triangles
If points P and Q are collinear with the centroid G, then P is the anticomplement of Q if G trisects segment PQ and is closer to Q than to P. See also complement. (According to Court, p. 297, the term anticomplementary point dates from 1886.)
Let L(A) be the line through vertex A parallel to side BC, and define L(B) and L(C) cyclically. Let A' = L(B)∩L(C), and define B' and C' cyclically. Then A'B'C' is the anticomplementary triangle of ABC. (Efforts to replace this name have encountered the fact that A' is the anticomplement of A.)
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-anticomplementary conjugate of U is the point
h(a,b,c,p,q,r,u,v,w) : h(b,c,a,q,r,p,v,w,u) : h(c,a,b,r,p,q,w,u,v),
where
h(a,b,c,p,q,r,u,v,w) = [b2/q(au + cw) + c2/r(au + bv) - a2/p(bv + cw)]/a.
Let f(X) be the anticomplement of X, given by
f(x : y : z) = (- ax + by + cz)/a : (ax - by + cz)/b : (ax + by - cz)/c,
and let k be P-isoconjugation. The P-anticomplementary conjugate of U is "what you do to f(X) to make f(k(X)) when f(X) = U."
If P = incenter, then P-anticomplementary conjugate is shortened to "anticomplementary conjugate."
Let P = p : q : r (barycentric coordinates) be a point not on a sideline of ABC and not X(4). The antigonal image of P is the point h(P) given by barycentyrics
h(a,b,c,p,q,r) : h(b,c,a,q,r,p) : h(c,a,b,r,p,q),
where
h(a,b,c,p,q,r) = p/[(b2 + c2 - a2)p2 - a2qr + (b2 - a2)pq + (c2 - a2)pr].
The point h(P) is the isogonal conjugate of the inverse-in-circumcircle of the isogonal conjugate of P. If P lies on the circumcircle then h(P)=X(4); otherwise, h(h(P))=P, so that h(P), in such a case, is called the antigonal conjugate of P. If P lies on the line at infinity, then h(P)=P.
Antigonal pairs of points are discussed in Jan Van Yzeren, "Pairs of Points: Antigonal, Isogonal, and Inverse," Mathematics Magazine 65 (1992) 339-347.
Subsequent developments occur in Hyacinthos, beginning with #7825.
Let P be a point not on a sideline of ABC. Let T = isotomic conjugate and S = Steiner- circumellipse-inverse (this ellipse is T of the line at infinity). The antitomic conjugate of P is the point T(S(T(P))). Source: Preamble just before X(14941).
See homologous images)
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-beth conjugate of U is the point
h(a,b,c,p,q,r,u,v,w) : h(b,c,a,q,r,p,v,w,u) : h(c,a,b,r,p,q,w,u,v),
where
h(a,b,c,p,q,r,u,v,w) = 2abcp(cos B + cos C)(ua'/p + vb'/q + wc'/r) - (a+b+c)a'b'c'u,
where a', b', c' are - a + b + c, a - b + c, a + b - c, respectively. Let f by the mapping given by
f(x : y : z) = p(y + z) : q(z + x) : r(x + y),
and let k be the mapping "reflection in the circumcenter." The P-beth conjugate of U is "what you do to f(X) to make
f(k(X)) when f(X) = U." (Hyacinthos #4146, Oct. 26, 2001.)
Let f(a,b,c) : f(b,c,a) : f(c,a,b) be a point that satisfies (1) in the definition of triangle center, but that |f(a,b,c)| ≠ |f(a,c,b)|. Then
f(a,c,b) : f(b,a,c) : f(c,b,a) and f(a,b,c) : f(b,c,a) : f(c,a,b)
are bicentric points, together comprising a bicentric pair. Example: the Brocard points, c/b : a/c : b/a and b/c : c/a : a/b.
See triangle center.
Let each of f(a,b,c) and g(a,b,c) be a center function (i.e., as in the definition of triangle center) or the zero function, such that one of these conditions holds:
(1) the degree of homogeneity of g equals that of f;Let
(2) f is the zero function and g is not the zero function;
(3) g is the zero function and f is not the zero function.
A' = f(a,b,c) : g(b,c,a) : g(c,a,b)
B' = g(a,b,c) : f(b,c,a) : g(c,a,b)
C' = g(a,b,c) : g(b,c,a) : f(c,a,b).
Then A'B'C' is the (f,g)-central triangle of type 1. A central triangle of type 1 is any triangle A'B'C' for which equations (1)-(3) hold for some choice of center functions f and g.
Next, suppose f and g are as for type 1 except that g(a,b,c) ≠ g(a,c,b). Let
A' = f(a,b,c) : g(b,c,a) : g(c,b,a)
B' = g(a,c,b) : f(b,c,a) : g(c,a,b)
C' = g(a,b,c) : g(b,a,c) : f(c,a,b).
Then A'B'C' is the (f,g)-central triangle of type 2. A central triangle of type 2 is any triangle A'B'C' for some choice of center function f and function g as described. Note that the coordinates in the definitions can be read as barycentrics without changing the classes of triangles called central, central of type 1, and central of type 2.
A form for compact notation for a central triangle is T(f(a,b,c), g(b,c,a)), where the triangle is of type 1 if g(b,c,a ) = g(b,a,c) and of type 2 otherwise; see the preamble to X(3758) in ETC.
Examples: ABC, the medial, orthic, excentral, anticomplementary, and tangential triangles are central of type 1; in fact, if X is a center, then the cevian and anticevian triangles of X are central of type 1. The pedal triangle of X is of type 2 if the triangle is not also a cevian triangle.
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-Ceva conjugate of U is the point
u(- qru + rpv + pqw) : v(qru - rpv + pqw) : w(qru + rpv - pqw),
which is the perspector of the cevian triangle of P and the anticevian triangle of U. (See cevian nest and cross conjugate.)
Ceva conjugate and cevapoint are related thus: X = P©U if and only if P = cevapoint(U,X), and in this case, U = P©X.
Let f(x : y : z) = p(y + z) : q(z + x) : r(x + y). The P-Ceva conjugate of U is "what you do to f(X) to make f(X -1) when f(X) = U." (Hyacinthos #3966, Sept. 26, 2001.)
If you have The Geometer's Sketchpad, you can view CEVA CONJUGATE.
Let P = p : q : r and U = u : v : w be distinct points, neither lying on a sideline of ABC. The cevapoint of P and U is the point
(pv + qu)(pw + ru) : (qw + rv)(qu + pv) : (ru + pw)(rv + qw).
Let A"B"C" be the anticevian triangle of U. Let A' =PA"∩BC, and define B' and C' cyclically. The cevapoint of P and U is the perspector, X, of triangles ABC and A'B'C'. Moreover, P is the X-Ceva conjugate of U, and U is the X-Ceva conjugate of P. (See cevian nest and Ceva conjugate.) As a comparison of cevapoint(P,U) and crosspoint(P,U), note that their trilinears can be written as
1/(qw + rv) : 1/(ru + pw) : 1/(pv + qu) and 1/qw + 1/rv : 1/ru + 1/pw : 1/pv + 1/qu.
If you have The Geometer's Sketchpad, you can view CEVAPOINT.
Floor Van Lamoen contributed the following two constructions of cevapoint(P,U). Let ApBpCp be the cevian triangle of P, and let AuBuCu be the cevian triangle of U. Define
| Apu = CpAu∩ApBu | . . . . . . . . . . . . . . | Aup = CuAp∩AuBp |
| Bpu = ApBu∩BpCu | . . . . . . . . . . . . . . | Bup = AuBp∩BuCp |
| Cpu = BpCu∩CpAu | . . . . . . . . . . . . . . | Cup = BuCp∩CuAp |
Then triangle ABC is perspective to both triangles ApuBpuCpu and AupBupCup, and the perspector in both cases is the cevapoint of P and U. (Received 10/17/2003)
Randy Hutson noted that cevapoint(P,U) is given by the following constructions:
* The intersection of tangents at P and U to the bianticevian conic of P and U;
* The crosspoint of P and U wrt both the anticevian triangle of P and anticevian triangle of U;
* The pole of line PU wrt the bianticevian conic of P and U. (Received 7/14/2019)
Let P be a point not on a sideline of ABC. The lines AP, BP, CP are the cevians of P.
Let D,E,F be triangles, where F is inscribed in E, and E is inscribed in D. If any two of the three triangles are perspective, then the ordered triple (D,E,F) is a cevian nest. (It is well known that if any two of the three triangles are perspective, then each is perspective to the third; in particular, E is a cevian triangle of D, and F is a cevian triangle of E.)
Cevian nests in which one of the triangles is ABC beget three families of conjugates: Ceva conjugates, cross conjugates, and isoconjugates. See also crosspoint.
If you have The Geometer's Sketchpad, you can view CEVIAN NEST.
Let P be a point not on a sideline of ABC. Let A' = AP∩BC meet. Define B' and C' cyclically. Triangle A'B'C' is the cevian triangle of triangle ABC.
If P = p : q : r, then A' = 0 : q : r, B' = p : 0 : r, C' = p : q : 0.
Examples of cevian triangles:
incentral triangle; P = incenter = X(1) = 1 : 1 : 1
medial triangle; P = centroid = X(2) = 1/a : 1/b : 1/c
orthic triangle; P = orthocenter = X(4) = sec A : sec B : sec C
intouch triangle; P = Gergonne point = X(7) = sec2(A/2) : sec2(B/2) : sec2(C/2)
extouch triangle; P = Nagel point = X(8) = csc2(A/2) : csc2(B/2) : csc2(C/2)
Let P = p : q : r be a point distinct from X(3). The circumperp conjugate of P is the point
f(p,q,r,a,b,c,SA,SB,SC) : f(q,r,p,b,c,a,SB,SC,SA) : f(r,p,q,c,a,b,SC,SA,SB),
where
f(p,q,r,a,b,c,SA,SB,SC) = (-a*(-b*c*SC*SB*p^2+2*r*q*SA^3)-SA*a*b*c*(b^2*q^2+c^2*r^2)+b*((SA+SB)*S^2-2*SA*SB^2)*r*p+c*((SC+SA)*S^2-2*SA*SC^2)*p*q)*a.
Let ABC be a triangle and P a point. The perpendicular bisectors of BC, CA, AB intersect the circumcircle at (A1, A2), (B1, B2), (C1, C2), respectively. Then the circumcircles of PA1A2, PB1B2, PC1C2 are coaxial. The other than P point of intersection of these circles is the circumperp conjugate of P, as A1, A2, B1, B2, C1, C2 are the vertices of the circumperp triangles. (See preamble just before X(18859))
Let P be a point not on a sideline of ABC, and let A'B'C' be the anticevian triangle of P. Let A" be the harmonic conjugate of A' with respect to B and C, and define B" and C" cyclically. (If P = p : q : r, then A" = 0 : y : - z.). The cocevian triangle of P is the triangle A"B"C". The vertices are collinear and the triangle degenerate. For a discussion, see TCCT, page 200.
Let P and U be finite points having normalized barycentric coordinates (p,q,r) and (u,v,w). Suppose that f = f(a,b,c) and g = g(a,b,c) are nonzero homogeneous functions having the same degree of homogeneity. Let x = fp + gu, y = fq + gv, z = fr + gw. The (f,g) combo of P and U, denoted by f*P + g*U, is the point X = x : y : z; the normalized barycentric coordinates of X are (kx,ky,kz), where k=1/(x+y+z).
The definition of combo readily extends to finite sets of finite points. In particular, the (f,g,h) combo of P = (p,q,r), U = (u,v,w), J = (j,k,m) is given by fp + gu + hj : fq + gv + hk : fr + gw + hm and denoted by f*P + g*U + h*J. Suppose that T is a (central) triangle with vertices A',B',C' given by normalize barycentrics. Then T is represented by a 3x3 matrix with row sums equal to 1. Let NT denote the set of these matrices and let * denote matrix multiplication. Then NT is closed under *. Also, NT is closed under matrix inversion, so that (NT, *) is a group. Once normalized, any central T can be used to produce triangle centers as combos of the form Xcom(nT); see the preambles to X(3663), X(3739), and X(3758) in ETC.
If points P and U are collinear with the centroid G, then P is the complement of U if G trisects segment PU and is closer to P than to U. See also anticomplement. (According to Court, p. 297, the term complementary point dates from 1885.)
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-complementary conjugate of U is the point
h(a,b,c,p,q,r,u,v,w) : h(b,c,a,q,r,p,v,w,u) : h(c,a,b,r,p,q,w,u,v),
where
h(a,b,c,p,q,r,u,v,w) = [b2/q(au - bv + cw) + c2/r(au + bv - cw)]/a.
Let f(X) be the complement of X, given by
f(x : y : z) = (bv + cw)/a : (cw + au)/b : (au + bv)/c,
and let k be P-isoconjugation. The P-complementary conjugate of U is "what you do to f(X) to make f(k(X)) when f(X) = U."
If P = incenter, then P-complementary conjugate is shortened to "complementary conjugate."
Let P = p : q : r and U = u : v : w be distinct points, neither lying on a sideline of ABC. The P-cross conjugate of U is the point
u/(- pvw + qwu + ruv) : v/(pvw - qwu + ruv) : w/(pvw + qwu - ruv).
Let A'B'C' be the cevian triangle of U. Let A" be where line PA' crosses line B'C', and define B" and C" cyclically - so that A"B"C" is the cevian triangle (in triangle A'B'C', not ABC) of P. The perspector of triangles ABC and A"B"C" is the P-cross conjugate of U. (See cevian nest.)
As a transformation, P-cross conjugate is an involution; i.e., if PxU = P-cross conjugate of U, then Px(PxU) = U. Properties of cross conjugates arise from those of Ceva conjugates; for, on writing PcU for the P-Ceva conjugate of U,
PxU = (U/P)*(UcP) and PcU = (U/P)*(UxP)
where / and * denote trilinear division and multiplication.
Cross conjugate and crosspoint are related thus: X = PxU if and only if P = crosspoint(X,U).
If you have The Geometer's Sketchpad, you can view CROSS CONJUGATE.
Let P = p : q : r and U = u : v : w be distinct points, neither lying on a sideline of ABC. The crossdifference of P and U is the point X defined by trilinears
qw - rv : ru - pw : pv - qu,
constructible as the isogonal conjugate of the trilinear pole of the line PU. Thus, U is the crossdifference of P and X, and P is the crossdifference of U and X. In order to see that the crossdifference of P and X is a solution for U of the equation
x : y : z = qw - rv : ru - pw : pv - qu,
note first that this equation implies px + qy + rz = 0. Thus, if u : v : w = qz - ry : rx - pz : py - qx, then
qw - rv = q(py - qx) - r(rx - pz) = - (p2 + q2 + r2)x, so that
qw - rv : ru - pw : pv - qu = x : y : z.
A point X is the crossdifference of distinct points P and U if and only if the line PU is the trilinear polar of the isogonal conjugate of X. Examples:
X(1) = crossdifference of X(44) and X(513)
X(2) = crossdifference of X(187) and X(512)
X(3) = crossdifference of X(230) and X(231).
Let W be the side-triangle of these two triangles: the cevian triangle of the isogonal conjugate of P and the cevian triangle of the isogonal conjugate of U. Then W is perspective to ABC, and the perspector is the crossdifference of P and U; see also crosspoint. (Randy Hutson, April 9, 2016)
Let P = p : q : r and U = u : v : w be distinct points, neither lying on a sideline of ABC. The crosspoint of P and U is the point
pu(rv + qw) : qv(pw + ru) : rw(qu + pv).
This point is introduced in TCCT with the notation C(P,Q). Here, "Q" is replaced by "U", and C(P,U) is abbreviated as X. The construction for X given in TCCT follows. Let A'B'C' be the cevian triangle of P and A"B"C" that of U. Let A''' = AA"∩B'C', and define B''' and C''' cyclically. Then X is the perspector of triangles A'B'C' and A'''B'''C'''. Moreover, U is the X-cross conjugate of P, and P is the X-cross conjugate of U. (See cevian nest and cross conjugate.) The following properties of X were noted by Jean-Pierre Ehrmann (5/29/03):
X = perspector of A'B'C' and the triangle with vertices AU∩B'C', BU∩C'A', CU∩A'B';
X = perspector of A"B"C" and the triangle with vertices AP∩B"C", BP∩C"A", CP∩A"B";
X = the point of concurrence of these three lines:
the line of points AP∩BU and AU∩BP
the line of points BP∩CU and BU∩CP
the line of points CP∩AU and CU∩AP
Figure 7.3 in TCCT with "Q" replaced by "U" can be used to visualize the nine lines concurring in X.
The lines tangent to the conic {A,B,C,P,U} at P and U intersect in X. (Randy Hutson, September 10, 2012)
Let W be the side-triangle of these two triangles: the cevian triangle of P and the cevian triangle of U. Let W' be the vertex-triangle of the anticevian triangle of P and the anticevian triangle of U. Then W is perspective to W', and the perspector is the crosspoint of P and U; see also crossdifference. (Randy Hutson, April 9, 2016)
If you have The Geometer's Sketchpad, you can view CROSSPOINT.
Let P = p : q : r and U = u : v : w be distinct points, neither lying on a sideline of ABC. The crosssum of P and U is the point X defined by trilinears
qw + rv : ru + pw : pv + qu,
constructible as the crosspoint of the isogonal conjugates of P and U. Thus, U is the isogonal conjugate of the X-cross conjugate of the isogonal conjugate of P, and P is the isogonal conjugate of the X-cross conjugate of the isogonal conjugate of U. (Regarding the neologism "crosssum" placed here on 5/28/03, what words in the English language have spellings containing three consecutive identical letters?)
A cubic is a curve of degree 3 in a,b,c. For a catalog with sketches, visit Bernard Gibert's site.
Let P = p : q : r be a point not on a sideline of ABC, and let A'B'C' be the cevian triangle of P. The circumcircle of A'B'C' meets line BC in two points: A' and A"; pairs B', B", and C',C" are obtained cyclically. The lines AA", BB", CC" concur in the cyclocevian conjugate of P. Let
g(a,b,c) = a/[p(qb + rc)] and f(a,b,c) = bc/[g(b,c,a) + g(c,a,b) - g(a,b,c)].
The cyclocevian conjugate of P is given by
f(a,b,c) : f(b,c,a) : f(c,a,b).
In Hyacinthos #6423 (January 24, 2003), Darij Grinberg states nine theorems, of which the last is as follows:
The cyclocevian conjugate of a point is the
isotomic conjugate
of the anticomplement
of the isogonal conjugate
of the complement
of the isotomic conjugate
of the point.
If you have The Geometer's Sketchpad, you can view CYCLOCEVIAN CONJUGATE.
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-daleth conjugate of U is the point
h(p,q,r,u,v,w) : h(q,r,p,v,w,u) : h(r,p,q,w,u,v),
where
h(p,q,r,u,v,w) = p(y/q - z/r)2 + x(2x/p - y/q - z/r).
Let DEF be a triangle in the plane of triangle ABC. Let D' be the isogonal conjugate of the point of intersection of line EF and the line at infinity. Define E' and F' cyclically. The triangle D'E'F' is the dual of DEF. The vertices of D'E'F' lie on the circumcircle, and D'E'F' is similar to DEF. The duality is between the sidelines EF, FD, DE and the points D', E', F', respectively. For example, if E and F remain fixed and D varies, then D' remains fixed, while E'F' varies. (From the preamble to X(2979) in ETC.)
Let T be a central triangle, and let U(T) be the unary cofactor triangle of T. Then T and U(T) are perspective, and their perspector is the eigencenter of T.
Suppose the A-, B-, C- vertices of T are Pi = xi : yi : zi, for i = 1,2,3. Let
s = y3(x1x2 + z1z2) - y1(x2x3 + z2z3)
t = z1(x2x3 + y2y3) - z2(x1x3 + y1y3)
u = z3(x1x2 + y1y2) - z1(x2x3 + y2y3)
v = y1(x2x3 + z2z3) - y2(x1x3 + z1z3)
Let x = st - uv, and define y and z cyclically. Then the eigencenter of T is the point x : y : z.
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-gimel conjugate of U is the point
h(a,b,c,p,q,r,u,v,w) : h(b,c,a,q,r,p,v,w,u) : h(c,a,b,r,p,q,w,u,v),
where
h(a,b,c,p,q,r,u,v,w) = abc[- (cos A)/p + (cos B)/q + (cos C)/r]S - 8uσ2,
where S = (bq + cr)u + (cr + ap)v + (ap + bq)w and σ = area of ABC.
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-he conjugate of U is the point
h(p,q,r,u,v,w) : h(q,r,p,v,w,u) : h(r,p,q,w,u,v),
where
h(p,q,r,u,v,w) = -p(y + z)2 + q(z + x)2 + r(x + y)2
+ (qr/p)(x + y)(x + z) - (rp/q)(y + z)(y + x) - (pq/r)(z + x)(z + y).
Let P = p : q : r and U = u : v : w be distinct points, neither lying on a sideline of ABC. The P-Hirst inverse of U is the point
qru2 - vwp2 : rpv2 - wuq2 : pqw2 - uvr2.
Geometrically, this is the point of intersection of the line PU and the polar of U with respect to the conic.
pyz + qzx + rxy = 0.
As a transformation, P-Hirst inverse is an involution; i.e., if PhU = P-Hirst inverse of U, then Ph(PhU) = U. Concerning the designation "Hirst inverse," see the information contributed by Gunter Weiss.
The term homologous means having the same relation or relative position to. Let T1 and T2 be two triangles, and P a point in the plane of triangle T1. The point P' in the plane of triangle T2 is a T1-to-T2 homologous image of P if P' has the same relation or relative position to T2 as P has to T1. However, the words "relation or relative position" are subject to different meanings, as discussed here.
If T1 and T2 are similar triangles, then P' is the T1-to-T2 similarity image of P.
Suppose that P has trilinears x : y : z wrt T1. Then the T1-to-T2 trilinear image of P is the point P' with trilinears x : y : z wrt T2. This is a non-affine collineation, preserving collinearities, but not ratios of distances between collinear points. Parallel lines do not remain parallel under this mapping, so that points on the line at infinity map to finite points. Circumconics of T1 map to circumconics of T2 and inconics of T1 map to inconics of T2.
Suppose that P has barycentrics x : y : z wrt T1. Then the T1-to-T2 barycentric image of P is the point P' with barycentrics x : y : z wrt T2. This is an affine collineation, preserving collinearities as well as ratios of distances between collinear points. Parallel lines remain parallel under this mapping, so that the line at infinity maps to itself. Conics map to conics of the same type (ellipses, including circles, map to ellipses, parabolas to parabolas, hyperbolas to hyperbolas). Circumconics of T1 map to circumconics of T2 and inconics of T1 map to inconics of T2.
Let the sidelengths of T1 be denoted a1, b1, c1 and the sidelengths of T2 be denoted a2, b2, c2. Suppose that P has coordinates f(a1,b1,c1) : g(b1,c1,a1) : h(c1,a1,b1) with respect to T1, where f, g, h either have the same degree of homogeneity, or else one is the zero function and the other two have the same degree of homogeneity. (If P is a center of T1, then f = g = h.) Then the T1-to-T2-functional image of P is the point P' with coordinates f(a2,b2,c2) : g(b2,c2,a2) : h(c2,a2,b2) with respect to T2. Coordinates here can be trilinears or barycentrics, as long as the same system is used for T1 and T2. P' serves the same 'function' wrt T2 (e.g., centroid, circumcenter, 1st Brocard point, A-vertex of orthic triangle, etc.) as P serves wrt T1. For example, the orthic-to-excentral functional image of X(5) is X(40), since X(5) and X(40) are the respective circumcenters of the orthic and excentral triangles. This is a non-affine collineation, preserving collinearities, but not ratios of distances between collinear points (except where these distance ratios define the point, such as midpoints, reflections, etc.). Parallel lines remain parallel under this mapping, so that the line at infinity maps to itself. Circles map to circles. Other conics map to conics, but not necessarily of the same type (e.g., the MacBeath circumconic of T1 may be an ellipse, but maps to the MacBeath circumconic of T2, which may be a hyperbola.) Circumconics of T1 map to circumconics of T2 and inconics of T1 map to inconics of T2.
Let P = p : q : r and U = u : v : w be points, neither on a sideline of ABC. The P-isoconjugate of U is the point
qrvw : rpwu : pquv.
Examples: the isogonal conjugate of U is the X(1)-isoconjugate of U, and the isotomic conjugate of U is the X(31)-isoconjugate of U.
As suggested by the meaning of the prefix "iso",
P-isoconjugate of U = U-isoconjugate of P.
Let A'B'C' be the anticevian triangle of U, and let A"B"C" be the anticevian triangle of P with respect to A'B'C'. The perspector of A'B'C' and A"B"C" is the U -2-isoconjugate of P, where U -2 = u -2 : v -2: w -2. (See cevian nest.)
The earliest appearance of the term "isoconjugate" in triangle geometry may be its inclusion in this Glossary as early as 1998. Isoconjugates are also discussed in C. Kimberling, "Conjugacies in the plane of a triangle," Aequationes Mathematicae 63 (2002) 158-167, submitted April 27, 1999, and "Conics associated with a cevian nest," Forum Geometricorum 1 (2001) 141-150.
Thereafter the term "isoconjugate" was sometimes used for reciprocal conjugate, a term defined in this Glossary, with a reference to probable earliest usage.
Let P = p : q : r be a point not on a sideline of ABC. Let L(A) be the line obtained by reflecting line AP in the internal bisector of angle A. Define L(B) and L(B) cyclically. The lines L(A), L(B), L(C) concur in the isogonal conjugate of P, which has trilinears 1/p : 1/q : 1/r and is denoted by P -1. See isoconjugate.
If you have The Geometer's Sketchpad, you can view ISOGONAL CONJUGATE and ISOGONAL CONJUGATE OF A LINE.
An isoscelizer is a line perpendicular to an angle bisector. If P is a point, then the A-isoscelizer of P is the line L(P,A) through P perpendicular to the line that bisects vertex angle A; the B- and C- isoscelizers are defined cyclically. Let D and E be the points where L(P,A) meets sidelines AB and AC. Unless D = E = A, the triangle ADE is isosceles.
In ETC, there are several triangle centers defined in terms of isoscelizers. These were discovered or invented by Peter Yff, in whose notebooks the word isoscelizer dates back to 1963.
Let P = p : q : r be a point not on a sideline of ABC. Let A', B', C' be the points where lines AP, BP, CP meet lines BC, CA, AB, respectively. Reflect A', B', C' about the midpoints of sides BC, CA, AB, respectively, to obtain points A", B", C". Then lines AA", BB", CC" concur in the isotomic conjugate of P, which has trilinears 1/(pa2) : 1/(qb2) : 1/(rc2). See isoconjugate.
A line is the set of points x : y : z satisfying the equation
f(a,b,c)x + g(a,b,c)y + h(a,b,c)z = 0
for some point f(a,b,c) : g(a,b,c) : h(a,b,c). If this point is a triangle center, then the corresponding line is a central line.
Three lines dx + ey + fz = 0, rx + sy + tz = 0, ux + vy + wz = 0 are concurrent if and only the following determinant equation holds:
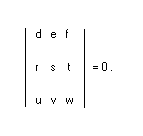
See also point.
Chapter 5 of TCCT discusses central lines.
Let P = p : q : r and U = u : v : w be distinct points, neither equal to A, B, or C. The P-line conjugate of U is the point
p(v2 + w2) - u(qv + rw) : q(w2 + u2) - v(rw + pu) : r(u2 + v2) - w(pu + qv),
or, equivalently,
hp - ku : hq - kv : hr - kw,
where h = u2 + v2 + w2 and k = pu + qv + rw.
This is the point of intersection of line PU and the trilinear polar of the isogonal conjugate of U.
Let Pi = xi : yi : zi, for i=1,2,3, be noncollinear points. An equation for line P2P3 is then
a1x + b1y + c1z = 0,
where a1 = y2z3 - z2y3, and b1 and c1 are defined cyclically. The trilinear pole of this line is the point
1/a1 : 1/b1 : 1/c1.
This point is the A-vertex of the line-polar triangle. The B- and C- vertices are defined cyclically.
A major center is a triangle center X for which there exists a function f(A) such that X = f(A) : f(B) : f(C). Examples: X(1), X(2), X(3), X(4), X(6). Major centers solve certain problems in functional equations; click here (AeqMath) or here (AMM) for more.
Let X = x : y : z be a point, and let
a1 = (b2 + c2 - a2)/(2bc) = cos A,
b1 = (c2 + a2 - b2)/(2ca) = cos B,
c1 = (a2 + b2 - c2)/(2ab) = cos C,
u1 = b1c1x3 - b1y3 - c1z3,
u2 = - (1 + 2c12)b1x2y - (1 + 2b12)c1x2z,
u3 = (2a1b1 - c1)y2z + (2a1c1 - b1)yz2,
u4 = 3b1c1xy2 + 3b1c1xz2,
u5 = (1 + b12 + c12 - a12 - 4a1b1c1)xyz,
f(a,b,c) = (- x + yc1 + zb1)(u1 + u2 + u3 + u4 + u5).
The orthojoin of X is the point f(a,b,c) : f(b,c,a) : f(c,a,b).
The above formula for f(a,b,c) can be written out explicitly in terms of a,b,c and simplified to the form
g(a,b,c) : g(b,c,a) : g(c,a,b), where
g(a,b,c) = bc[2abcx + c3y + b3z - (a2 + bc)(cy + bz)]F,
where F = x[a4 - (b2 - c2)2] + 2a[by(b2 - a2 - c2) + cz(c2 - b2 - a2)]
The orthojoin of X, defined (6/16/03) as above, can be described geometrically (when a,b,c are sidelengths of a triangle) as the orthopole of the trilinear polar of the isogonal conjugate of X. The orthopole of a line L is constructed as follows. Let A' be the foot of the perpendicular from vertex A on L, and define B' and C' cyclically. Then the perpendiculars from A' to BC, from B' to CA, and from C' to AB concur in the orthopole of L. For a proof and link to further information, see Orthopole - a new proof by Darij Grinberg.
Each point X on the line at infinity is the point common to every line in a family F(X) of pairwise parallel lines. That is, X may be regarded as the direction common to the lines in F(X). Let L be any line in F(X), and let L' be any line perpendicular to L. Let G be the family of lines parallel to L'. The orthopoint of X is the point H(X) in which L' meets the line at infinity. If X = x : y : z, then
H(X) = cy cos B - bz cos C : az cos C - cx cos A : bx cos A - ay cos B.
For any X on the line at infinity, the isogonal conjugates of X and H(X) are circumcircle-antipodes; i.e., each is the X(3)-reflection of the other.
Triangles DEF and UVW are perspective triangles if one of the following six triples of lines concur in a point:
{DU,EV,FW}, {DV,EW,FU}, {DW,EU,FV}; {DU,EW,FV}, {DV,EU,FW}, {DW,EV,FU}
The point of concurrence is called a perspector (replacing center of perspective). If, for example, lines DU,EV,FW concur in a point, then by Desargues's theorem, the points
EF intersect VW, FD intersect WU, DE intersect UV
are collinear, and their line is the perspectrix (replacing axis of perspective.)
In case DEF is the reference triangle, ABC, and UVW is a central triangle, it is sometimes tacitly understood that perspectivity of the two triangles refers to only one of the six possibilities, namely, the concurrence of lines DU,EV,FW. In this case, if UVW is the cevian triangle, A'B'C', of a point P, then P is the perspector of ABC and A'B'C', and the perspectrix is the trilinear polar of P.
In traditional euclidean geometry, point is not subject to definition, much as an axiom is not subject to proof. However, when (a,b,c) is variable or indeterminate, a point is defined informally by f(a,b,c) : g(a,b,c) : h(a,b,c) for all (a,b,c) for which at least one of the values f(a,b,c), g(a,b,c), h(a,b,c) is not zero. A formal definition is given in TCCT. See also triangle center.
Three points x : y : z, r : s : t, u : v : w are collinear if and only the following determinant equation holds:
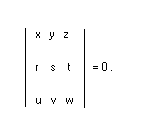
Thus, if x : y : z is a variable point, this equation gives the line determined by the points r : s : t and u : v : w.
Let Pi = xi : yi : zi, for i = 1,2,3, be noncollinear points, none lying on a sideline of ABC. The trilinear polar of P1 is the line
x/x1 + y/y1 + z/z1 = 0,
and the trilinear polars of P2 and P3 are defined cyclically. These last two lines meet in the point
1/y2z3 - 1/z2y3 : 1/z2x3 - 1/x2z3 : 1/x2y3 - 1/y2x3.
This point is the A-vertex of the point-polar triangle. The B- and C- vertices are defined cyclically.
Let W be a conic, P a point, and XX' and YY' chords of W that meet in P. As X and Y vary, the locus of the point X'Y∩XY' is a line, called the polar of P with respect to W. If W is a circumconic, it has an equation uyz + vzx + wxy = 0, and the polar of a point Q = p : q : r is the line
(vr + wq)x + (wp + ur)y + (uq + vp)z = 0.
A triangle center X is a polynomial center if there exists a polynomial f(a,b,c) such that
X = f(a,b,c) : f(b,c,a) : f(c,a,b).
Examples: X(1), X(2), . . . , X(12), but not X(13).
The radical trace of two nonconcentric circles is the point of intersection of the radical axis of the circles and the line of the centers of the circles. (For examples, see X(I) for I = 6, 187, 1570, 2021-2025, 2030-2032.)
Let P and U be points, neither on a sideline of ABC, given in barycentric coordinates by P = p : q : r and U = u : v : w. The P-reciprocal conjugate of U is the point
pvw : qwu : ruv. (barycentrics)
As suggested by the meaning of "reciprocal",
P-reciprocal conjugate of U = G/(U-reciprocal conjugate of P),
in accord with the fact that G, the centroid, is the identity corresponding to barycentric division.
The term reciprocal conjugate was introduced in Keith Dean and Floor van Lamoen, "Geometric construction of reciprocal conjugations," Forum Geometricorum 1 (2001) 115-120.
See also isoconjugate.
Let p(a, b, c), q(a, b, c), r(a, b, c) be functions of a, b, c, all of the same degree of homogeneity. As the plane consists of points [functions of the form X = x(a, b, c) : y(a, b, c) : z(a, b, c)], the substitution indicated by
a → p(a, b, c), b → q(a, b, c), c → r(a, b, c)
maps the set of all points - that is, the plane - into itself. Such a substitution has no clear geometric meaning, as suggested by the name, symbolic substitution. On the other hand, symbolic substitutions are of geometric interest because they map lines to lines, conics to conics, cubics to cubics, and they preserve incidence.
Example: The symbolic substitution (a, b, c) →(1/a, 1/b, 1/c) maps every triangle center to a triangle center, every pair of bicentric points to a pair of bicentric points, every circumconic to a circumconic, etc. However, when (a, b, c) = (2, 4, 5), for example, then a, b, c are sidelengths of a euclidean triangle, but 1/a, 1/b, 1/c are not.
Symbolic substitutions are introduced in C. Kimberling, "Symbolic substitutions in the transfigured plane of a triangle," Aequationes Mathematicae 73 (2007) 156-171.
Let P = p : q : r (barycentric coordinates) be a point not on a sideline of ABC, not X(3), and not on the circumcircle of ABC. The syngonal image of P is the point k(P) given by barycentyrics
k(a,b,c,p,q,r) : k(b,c,a,q,r,p) : k(c,a,b,r,p,q),
where
k(a,b,c,p,q,r) = (q + r - p)/[2a2qr - (q + r - p)(b2r + c2q)].
The point k(P) is the antigonal image of the anticomplement of P. For further developments, search Hyacinthos for "symgonal" - however, following Hyacinthos #9881, the spelling "syngonal" is used here.
A triangle center X is a transcendental center if there exists no algebraic function f(a,b,c) such that X = f(a,b,c) : f(b,c,a) : f(c,a,b). Examples: X(359) and X(360).
A triangle center is a point of the form f(a,b,c) : f(b,c,a) : f(c,a,b), where f is a nonzero function satisfying two conditions:
(1) f is homogeneous in a,b,c; i.e., there is a nonnegative real number h such that
f(ta,tb,tc) = thf(a,b,c) for all (a,b,c) in the domain of f;
(2) f is symmetric in b and c; i.e., f(a,c,b) = f(a,b,c).
A formal definition of triangle center is given in TCCT. See also polynomial center, transcendental center, central triangle, bicentric points.
The trilinear polar of a point p : q : r is the line
qrx + rpy + pqz = 0.
The trilinear pole of the line ux + vy + wz = 0 is the point wv : uw : uv.
Geometrically, the trilinear pole of a line PU is the perspector of ABC and the vertex-triangle of the anticevian triangles of P and U. (Randy Hutson, April 9, 2016)
Let Pi = xi : yi : zi, for i=1,2,3, be points. The A-vertex of the unary cofactor triangle is the point
y2z3 - z2y3 : z2x3 - x2z3 : x2y3 - y2x3 .
The B-vertex and C-vertex are defined cyclically. The vertices are the isogonal conjugates of the the vertices of the line-polar triangle of the points Pi.
If T is a triangle and U(T) its unary cofactor triangle, then U(U(T)) = T, and T and U(T) are perspective; see eigencenter.
The U-vertex conjugate of X is defined for distinct points U = u : v : w and X = x : y : z: (trilinears) as the point P given by
P = a/[a2vwyz - ux(bw + cv)(bz + cy)] : b/[b2wuzx - vy(cu + aw)(cx + az)] : c/[c2uvxy - wz(av + bu)(ay + bx)].
Suppose that T = DEF and T' = D'E'F' are triangles. The vertex triangle of T and T' is the triangle V(T,T') having sidelines DD', EE', FF'. Thus, V(T,T') generalizes "perspector", since V(T,T') is a single point if and only if T is perspective to T'. If U and X are distinct points, then (vertex triangle of the circumcevian triangles of U and X) is perspective to ABC, and the perspector is the U-vertex conjugate of X, which equals the X-vertex conjugate of U. See C. Kimberling, Mappings Associated with Vertex Triangles, Forum Geometricorum, 2 (2002) 21-32.
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-waw conjugate of U is the point
h(p,q,r,u,v,w) : h(q,r,p,v,w,u) : h(r,p,q,w,u,v),
where
h(p,q,r,u,v,w) = p[x2q2r2 + 2p2(ry - qz)2 - pqr2xy - pq2rxz]
Let P = p : q : r and U = u : v : w be points, neither lying on a sideline of ABC. The P-zayin conjugate of U is the point
h(p,q,r,u,v,w) : h(q,r,p,v,w,u) : h(r,p,q,w,u,v),
where
h(p,q,r,u,v,w) = p(y + z)2 - ry2 - qz2 + (p - r)xy + (p - q)xz.
Note that X(1)-zayin conjugacy is simply isogonal conjugacy.