YFF CENTER OF CONGRUENCE

Let P2Q3 (that's P with a subscript of 2, etc.) be an isoscelizer of angle A in triangle ABC; this means that AP2Q3 is an isosceles triangle. Let P3Q1 and P1Q2 be isoscelizers of angles B and C, respectively. Let A', B', C' be the vertices of the triangle formed by the three isoscelizers.

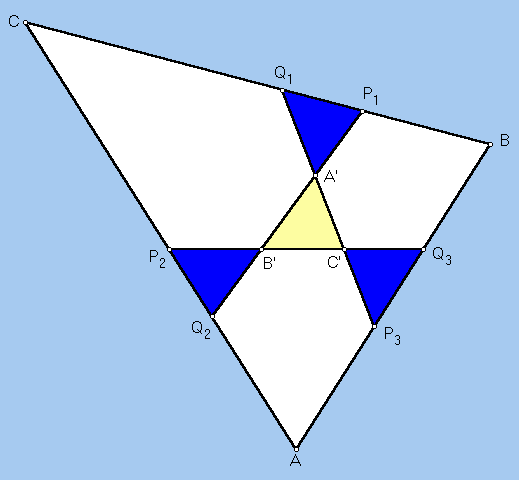
Peter Yff proved in 1987 that the six points P1, P2, P3, Q1, Q2, Q3 can be constructed so that the four triangles P1Q1A', P2Q2B', P3Q3C', A'B'C' are congruent. The three isoscelizers can then be continuously lengthened in such a way that the triangle A'B'C' shrinks to a single point, here named the Yff center of congruence. Yff also proved that trilinears for this point are

sec(A/2) : sec(B/2) : sec(C/2).

(For a quick lesson on trilinears, click on TRILINEAR COORDINATES.)

Triangle Centers
Clark Kimberling Home Page