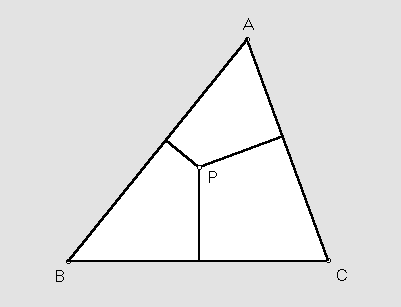
|
Suppose P is a point in the plane of a triangle ABC. Any three numbers proportional to the directed distances from P to the sidelines BC, CA, AB, in that order, are called homogeneous trilinear coordinates for P. Often the word homogeneous is omitted, or the whole thing is shortened to trilinears.
The incenter of triangle ABC, for example, being equidistant from the sidelines, has trilinears 1 : 1 : 1. The vertices themselves are given especially simply by
A = 1 : 0 : 0, The best known triangle centers all have remarkably simple trilinears. See for yourself: |
|
incenter = 1 : 1 : 1
centroid = csc(A) : csc(B) : csc(C) = 1/a :1/b : 1/c, where a, b, c are the sidelengths of triangle ABC
circumcenter = cos(A) : cos(B) : cos(C)
orthocenter = sec(A) : sec(B) : sec(C)
nine-point center = cos(B - C) : cos(C - A) : cos(A - B)
symmedian point (Lemoine point) = sin(A) : sin(B) : sin(C)
Gergonne point = [sec(A/2)]^2 : [sec(B/2)]^2 : [sec(C/2)]^2
Nagel point = [csc(A/2)]^2 : [csc(B/2)]^2 : [csc(C/2)]^2
Feuerbach point = 1 - cos(B - C) : 1 - cos(C - A) : 1 - cos (A - B)
Fermat point = csc(A + pi/3) : csc(B + pi/3) : csc(C + pi/3)
1st isodynamic point = sin(A + pi/3) : sin(B + pi/3) : sin(C + pi/3)
1st Napoleon point = csc(A + pi/6) : csc(B + pi/6) : csc(C + pi/6)
C. Kimberling, "Central points and central lines in the plane of a triangle," Math. Mag. 67 (1994) 163-187.
Properties of trilinear coordinates are presented in
H. S. M. Coxeter, "Some applications of trilinear coordinates," Linear Algebra and Its Applications 226-228 (1995) 375-388.
Closely related to homogeneous trilinear coordinates are homogeneous barycentric coordinates. If r : s : t are trilinears for a point P, then r sin(A) : s sin(B) : t sin(C) are barycentrics for P.