1/(cos(B) + cos(C)) :
1/(cos(C) + cos(A)) :
1/(cos(A) + cos(B)),
or, equivalently,
(b + c - a)/(b + c) :
(c + a - b)/(c + a) :
(a + b - c)/(a + b),
where a, b, c denote the sidelengths of triangle ABC.
|
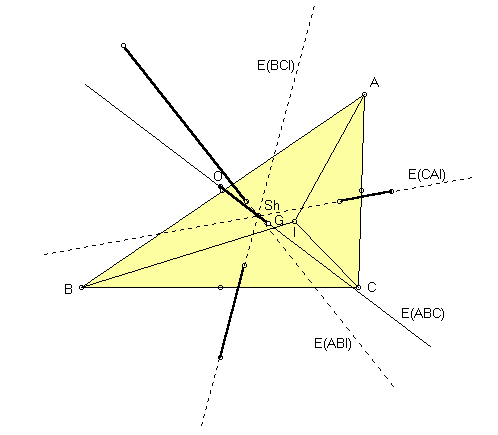
Let I denote the incenter of a triangle ABC. The Schiffler point of ABC is the point of concurrence of the Euler lines of the four triangles BCI, CAI, ABI, ABC. Trilinear coordinates for the Schiffler point are
1/(cos(B) + cos(C)) : or, equivalently,
(b + c - a)/(b + c) : where a, b, c denote the sidelengths of triangle ABC. |

|
(For a quick lesson on trilinears, click on TRILINEAR COORDINATES.)
The Schiffler point is named for Kurt Schiffler (1896-1986), who introduced the point in a problem proposal. The solvers, named below, suggested that the point be named the Schiffler point.
Kurt Schiffler, G. R. Veldkamp, and W. A. van der Spek, Problem 1018 and Solution, Crux Mathematicorum 12 (1986) 176-179.