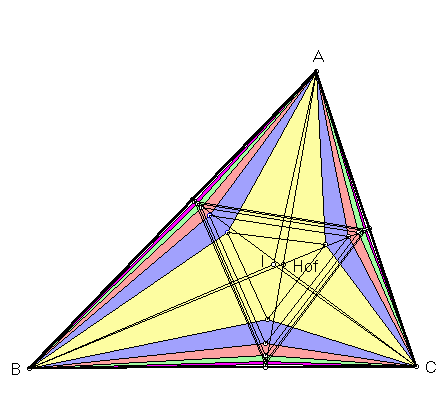
| The Hofstadter points are defined from Hofstadter triangles, so we begin by constructing the latter from a reference triangle ABC. For any nonzero real number r, swing line segment BC about pivot B toward vertex A through angle rB. (For example, if r = 1/2, then the swung segment bisects angle B.) Let L denote the line containing the swung segment. Similarly, obtain line L' by swinging segment BC about C through angle rC. Let A(r) be the point of intersection of lines L and L'. Points B(r) and C(r) are formed analogously. The triangle with vertices A(r), B(r), C(r) is the r-Hofstadter triangle. |

|
In
C. Kimberling, "Hofstadter points," Nieuw Archief voor Wiskunde 12 (1994) 109-114,
it is proved that the r-Hofstadter triangle is perspective to triangle ABC, and that the center of perspective is given by trilinear coordinates
sin(rA)/sin(A - rA) :
sin(rB)/sin(B - rB) :
sin(rC)/sin(C - rC).
Taking the limit as r approaches zero defines the Hofstadter zero-point, possibly first discovered in 1992 by Douglas Hofstadter (winner of a 1980 Pulitzer Prize for his book Gödel, Escher, Bach: an Eternal Golden Braid). Trilinear coordinates for this point are especially notable, since they cannot be expressed as algebraic functions of the sidelengths a, b, c of the reference triangle. Here are trilinears:
A/a : B/b : C/c.
Taking the limit of trigonometric trilinears as r approaches 1 yields the Hofstadter one-point, with equally intriguing trilinears:
a/A : b/B : c/C.
(For a quick lesson on trilinears, click on TRILINEAR COORDINATES.)