In 1998, John Conway noted that the version of Gossard's theorem in Cajori's A History of Mathematics is ambiguous. In a corrected version, he introduced the term Gossard perspector:
The Euler lines of the three triangles obtained by taking the Euler line and two sides of ABC form a triangle Ag Bg Cg congruent to ABC and sharing its Euler line. In fact Gossard's triangle is the reflection of ABC in a point that I therefore call "the Gossard Perspector" Pg.
|
|
The earliest published mention of the Gossard configuration, which includes the Gossard perspector, occurs in a summary of a meeting of the Southwestern Section of the American Mathematical Society. Written in the Bulletin of the American Mathematical Society 22 (1916) 218-219 by the Secretary of the Section, the exact wording is as follows:
Euler proved that orthocenter, circumcenter, and centroid of a triangle are collinear, and the line through them has received the name "Euler line." He also proved that the Euler line of a given triangle together with two of its sides forms a triangle whose Euler line is parallel with the third side of the given triangle. By the use of vector coordinates or ordinary projective coordinates, Professor Gossard proves the following theorem: the three Euler lines of the triangles formed by the Euler line and the sides, taken by twos, of a given triangle, form a triangle triply perspective with the given triangle and having the same Euler line. The orthocenters, circumcenters and centroids of these two triangles are symmetrically placed as to the center of perspective.In December, 1999, Paul Yiu gave a generalization of Gossard's theorem and perspector. 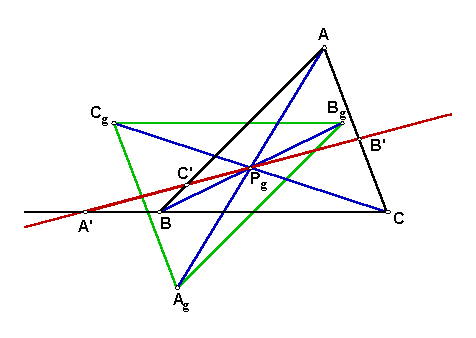With his permission, Yiu's generalization follows: Let P be a point other than the centroid, G, of a triangle ABC. Let X = PG^BC, Y = PG^CA, Z = PG^AB. Let Ga, Gb, Gc be the centroids of triangles AYZ, BZX, CXY, respectively. Let Pa be the point such that line lines Y-to-Pa and BP are parallel and lines Z-to-Pa and CP are parallel. Define points Pb and Pc cyclically. Then the triangle A'B'C' formed by the lines Ga-to-Pa, Gb-to-Pb, Gc-to-Pc is congruent and inversely homothetic to ABC, and the center of homothety (i.e., the perspector), is on the line GP. If P is the orthocenter in Yiu's generalization, then A'B'C' is the Gossard triangle and the center of homothety is the Gossard perspector. If P is given in homogeneous barycentric coordinates as P = f : g : h, then the general perspector is given by first barycentric coordinate (g + h - 2f)(g^2 + h^2 - f^2 - 3gh + hf + fg); On taking f = tan A, g = tan B, h = tan C, one can write out barycentrics (and trilinears) for the Gossard perspector.
Harry Clinton Gossard, educator, geometer
|
