|
The most famous line in the subject of triangle geometry is the Euler line, named in honor of Leonhard Euler (pronounced Oiler), who penned more pages of original mathematics than any other human being.
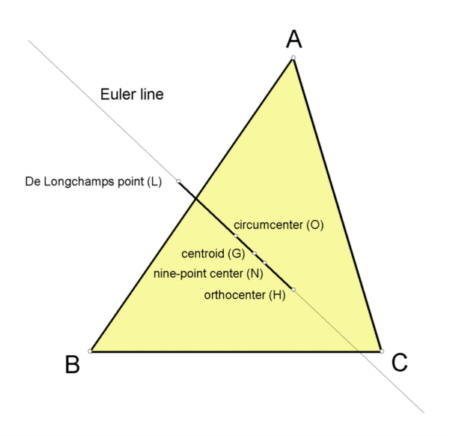
Suppose ABC is a triangle. Let G = centroid of ABC, and O = circumcenter of ABC. The line GO is the Euler line of ABC. Let H, N, and L denote the orthocenter, nine-point center, and DeLongchamps point of ABC, respectively. These three well-known points also lie on the Euler line. In fact - and this is what really makes the Euler line so famous - when you vary the shape of triangle ABC, the relative distances between the points G, O, H, N, L remain the same:
|
|
There are also many other interesting points on the Euler line. Most of them were first studied after 1980. They will be identified here by trilinear coordinates, written in the form x : y : z. For example,
centroid = 1/a : 1/b : 1/c
circumcenter = cos(A) : cos(B) : cos(C).
Trilinears x : y : z of a point P are any numbers (or functions of the sidelengths a,b,c of triangle ABC) that are proportional to the directed distances from P to the sidelines BC, CA, AB, respectively. In addition to representations by trilinears, the index i for points listed in the book, Triangle Centers and Central Triangles, or simply TCCT, will be given by the notation X(i). For example, centroid = X(2).
Part 1. Centers listed in TCCT (Chapters 3, 4, 9)
X(2) = 1/a : 1/b : 1/c = bc : ca : ab = csc(A) : csc(B) :csc(C) = centroid
X(3) = cos(A) : cos(B) : cos(C) = circumcenter
X(4) = sec(A) : sec(B) : sec(C) = orthocenter
X(5) = cos(B - C) : cos(C - A) : cos(A - B) = nine-point center
The above examples indicate that if you know the first coordinate, you can easily write out the other two coordinates. To save space, the other two coordinates will be abbreviated as ": :".
X(20) = cos A - cos B cos C : : = DeLongchamp point
X(21) = 1/(cos B + cos C) : : = Schiffler point
X(22) = a(b^4 + c^4 - a^4) : : = Exeter point
X(23) = a(b^4 + c^4 - a^4 - b^2 c^2) : : = far-out point
X(24) = sec A cos 2A : : = perspector of ABC and orthic-of-orthic triangle
X(25) = sin A tan A : : = homothetic center of orthic and tangential triangles
X(26) = a(b^2 cos 2B + c^2 cos 2C - a^2 cos 2A) : : = circumcenter of tangential triangle
X(27) = (sec A)/(b + c) : :
X(28) = (tan A)/(b + c) : :
X(29) = (sec A)/(cos B + cos C) : :
X(30) = cos A - 2 cos B cos C : : = Euler infinity point
X(140) = bc [b cos(C - A) + c cos(B - A)] : : = nine-point center of medial triangle
X(186) = 4 cos A - sec A : : = inverse of X(4) in circumcircle
X(199) = a [b^4 + c^4 - a^4 + (b^2 + c^2 - a^2)(bc + ca + ab)] : :
X(235) = (cos^2 B + cos^2 C) sec A : : = midpoint of segment X(4)-to-X(24)
X(237) = sin^2 A cos(A + w) : : where w = Brocard angle of ABC
X(297) = csc^2 A cos(A + w) : : where w = Brocard angle of ABC
X(376) = csc A (5 sin 2A - sin 2B - sin 2C) : : = reflection of X(2) about X(3)
X(377) = bc [b^4 + c^4 - a^4 - 2 b^2 c^2 - 2 abc(a + b + c)] : :
X(378) = sec A + 2 cos A : : = harmonic conjugate of X(24) w.r.t. X(3) and X(4)
X(379) = bc [a^5 + (b + c)(a^2 bc - (b - c)^2 (bc + ca + ab))] : :
X(381) = cos A + 4 cos B cos C : : = midpoint of segment X(2)-to-X(4)
X(382) = cos A - 4 cos B cos C : :
X(383) = csc(B - C)[sin 2B sin(C - w) sin(C + pi/3) - sin 2C sin(B - w) sin(B + pi/3) : :
X(384) = a^3 + (b^2)(c^2)/a : : = Conway point
Part 2. "New" Centers, not listed in TCCT (most of them found after 1998)
X(401) = (csc A)(sin 2B sin 2C - sin 2A sin 2A) : : = Bailey point
X(402) = [trilinears omitted] = Gossard perspector
X(403) = (sec A)(1 + cos 2B + cos 2C) : : = X(36) of orthic triangle
X(404) = bc(a + b + c) - a(b^2 + c^2 - a^2) : : = harmonic conjugate of X(21) w.r.t. X(2) and X(3)
X(405) = (a + b + c)/a + cos A : :
X(406) = (a + b + c)/a + sec A : :
X(407) = (y + z) sec A : : , where x : y : z = X(21)
X(408) = (y + z) cos A : : , where x : y : z = X(29)
X(409) = x^2 + yz : : , where x : y : z = X(21)
X(410) = x^2 + yz : : , where x : y : z = X(29)
X(411) = (1/y)^2 + (1/z)^2 - (1/x)^2 : : , where x : y : z = X(21)
X(412) = (1/y)^2 + (1/z)^2 - (1/x)^2 : : , where x : y : z = X(29)
X(413) = x^3 (y^2 + z^2 - yz) : : , where x : y : z = X(21)
X(414) = x^3 (y^2 + z^2 - yz) : : , where x : y : z = X(29)
X(415) = (x^2 - yz) sec A : : , where x : y : z = X(21)
X(416) = (x^2 - yz) cos A : : , where x : y : z = X(29)
X(417) = (y^2 + z^2) cos A : : , where x : y : z = X(4)
X(418) = (csc 2B + csc 2C) cos A : :
X(419) = (x^2 - yz) sec A : : , where x : y : z = X(31)
X(420) = (x^2 - yz) sec A : : , where x : y : z = X(38)
X(421) = (x^2 - yz) sec A : : , where x : y : z = X(47)
X(422) = (x^2 - yz) sec A : : , where x : y : z = X(58)
X(423) = (x^2 - yz) sec A : : , where x : y : z = X(81)
X(424) = (x^2 - yz) sec A : : , where x : y : z = X(191)
X(425) = (x^2 - yz) sec A : : , where x : y : z = X(283)
X(426) = (y^2 + z^2) cos A : : , where x : y : z = X(19)
X(427) = (y + z) sec A : : , where x : y : z = X(31)
X(428) = (y + z) sec A : : , where x : y : z = X(38)
X(429) = (y + z) sec A : : , where x : y : z = X(58)
X(430) = (y + z) sec A : : , where x : y : z = X(81)
X(431) = (y + z) sec A : : , where x : y : z = X(283)
X(432) = (y^2 + z^2) sec A : : , where x : y : z = X(155)
X(433) = (y^2 + z^2) sec A : : , where x : y : z = X(159)
X(434) = (y^2 + z^2) sec A : : , where x : y : z = X(195)
X(435) = (y^2 + z^2) sec A : : , where x : y : z = X(399)
X(436) = sec A (sin^2 2A + sin 2B sin 2C) : :
X(437) = (x^2 + yz) sec A : : , where x : y : z = X(214)
X(438) = (x^2 + yz) csc A : : , where x : y : z = X(204)
X(439) = a(x^2) : : , where x : y : z = X(193)
X(440) = (y + z)/a : : , where x : y : z = X(28)
X(441) = (y + z)/a : : , where x : y : z = X(240)
X(442) = (y + z)/a : : , where x : y : z = X(284)
X(443) = (y + z)/a : : , where x : y : z = X(380)
X(444) = (y + z) tan A : : , where x : y : z = X(256)
X(445) = (y + z) csc 2A : : , where x : y : z = X(79)
X(446) = x (y^2 + z^2) : : , where x : y : z = X(98)
X(447) = (x^2 - yz)/a : : , where x : y : z = X(28)
X(448) = (x^2 - yz)/a : : , where x : y : z = X(284)
X(449) = (x^2 - yz)/a : : , where x : y : z = X(380)
X(450) = sec A (cos^4 A - cos^2 B cos^2 C) : : , X(3)-diamond conjugate of X(4)
X(451) = x sec A : : , where x : y : z = X(191)
X(452) = x csc A : : , where x : y : z = X(380)
X(453) = (x^2)/(cos B + cos C) : : , where x : y : z = X(46)
X(454) = (x^2) sec A : : , where x : y : z = X(155)
X(455) = (x^2) sec A : : , where x : y : z = X(159)
X(456) = (x^2) sec A : : , where x : y : z = X(195)
X(457) = (x^2) sec A : : , where x : y : z = X(399)
X(458) = x csc 2A : : , where x : y : z = X(182)
X(459) = x tan A : : , where x : y : z = X(193)
X(460) = x tan A : : , where x : y : z = X(230)
X(461) = x tan A : : , where x : y : z = X(391)
X(462) = x tan A : : , where x : y : z = X(395)
X(463) = x tan A : : , where x : y : z = X(396)
X(464) = x cot A : : , where x : y : z = X(387)
X(465) = x cot A : : , where x : y : z = X(397)
X(466) = x cot A : : , where x : y : z = X(398)
X(467) = x csc 2A : : , where x : y : z = X(52)
X(468) = x csc 2A : : , where x : y : z = X(187)
X(469) = x csc 2A : : , where x : y : z = X(386)
X(470) = sin(A + pi/3) csc 2A : :
X(471) = sin(A - pi/3) csc 2A : :
X(472) = cos(A + pi/3) csc 2A : :
X(473) = cos(A - pi/3) csc 2A : :
Several patterns can be noted in Part 2 of the above list. One of the most striking is the role of the Schiffler point X(21) and the unnamed point X(29) in the constructions of points X(407) to X(416). Letting I = incenter, the Schiffler point is where the Euler lines of triangles ABC, BCI, CAI, and ABI meet. No analogous property is known for X(29), but it would seem, nonetheless, that X(29) must be a close cousin of X(21).
More gleanings from Part 2 of the above list
The list suggests that a point (y + z) sec A : : is on the Euler line if and only if the point (x^2 - yz) sec A : : is on the Euler line. An easy proof depends on the fact that both conditons are equivalent to the equation
(y - z)(cos A)^2 + (z - x)(cos B)^2 + (x - y)(cos C)^2 = 0.
It is also easy to prove that a point (x^2) sec A : : is on the Euler line if and only if the point (y^2 + z^2) sec A : : is on the Euler line. Likewise, a point (y + z)/a : : is on the Euler line if and only if the point (x^2 - yz)/a : : is on the Euler line.
Hard to prove chain of distance inequalities
The aforementioned book, TCCT, catalogues 400 triangle centers, X(1), X(2),...,X(400). In Chapter 9, a chain of 46 distance inequalities is stated. These were found and tested on thousands of triangles by computer. Proofs of some of these would probably be elaborate and lengthy.
Let D(i) = signed distance from center X(i) to the Euler line, with D(i) > 0 if X(i) lies on the same side of the Euler line as X(1), the incenter. A reduced chain involving well known points is the following:
D(8)<=D(9)<=D(10)<=D(2)<=D(1)<=D(7)<=D(6)<=D(14).
Here, D(2) = 0, since X(2) is the centroid, lying on the Euler line. Here's how to interpret this chain of 7 inequalities: in every triangle, the Nagel point, X(8), is never closer to the Euler line than the Mittenpunkt, X(9), which is never closer than the Spieker center, which is always separated by the Euler line from the incenter, X(1), which is never farther from the Euler line than the Gergonne point, X(7), which is never farther than the symmedian point, X(6), which is never farther than the 2nd isogonic center, X(14).
Here's the whole chain listed in TCCT:
D(84)<=D(346)<=D(306)<=D(69)<=D(314)<=D(76)<=D(319)<=D(144)<=D(8)<=D(321)<=D(63)
<=D(333)<=D(75)<=D(210)<=D(40)<=D(71)<=D(9)<=D(10)<=D(164)<=D(165)<=D(167)
<=D(2)<=D(178)<=D(45)<=D(38)<=D(37)<=D(55)<=D(260)<=D(226)<=D(1)<=D(176)
<=D(174)<=D(7)<=D(177)<=D(180)<=D(173)<=D(81)<=D(61)<=D(39)<=D(6)<=D(58)<=D(32)
<=D(62)<=D(14)<=D(44)<=D(148)<=D(239).
Four central lines parallel to the Euler line
L(11,36) - that's the line determined by the triangle centers X(11) and X(36)
L(12,35)
L(13,15)
L(14,16).
The points referred to are indexed and identified (in TCCT) as follows:
X(11) = Feuerbach point = 1 - cos(B - C) : :
X(12) = (a harmonic conjugate of X(11)) = 1 + cos(B - C) : :
X(13) = Fermat point = 1st isogonic point = csc(A + pi/3) : :
X(14) = 2nd isogonic point = csc(A - pi/3) : :
X(35) = (a harmonic conjugate of X(36)) = 1 + 2 cos A : :
X(36) = inverse of incenter in circumcircle = 1 - 2 cos A : : .
Ten central lines perpendicular to the Euler line
Let x : y : z be trilinears for a variable point in the plane of a triangle ABC. Then an equation for the Euler line is
sin 2A sin(B - C) x + sin 2B sin(C - A) y + sin 2C sin(A - B) z = 0.
If someone just told you the first coefficient, namely sin 2A sin(B - C), you could easily write out the rest of the equation. The method of doing so shows that the somewhat lengthy equation can be abbreviated to sin 2A sin(B - C) x + ... = 0. Using this notation, another equation for the Euler line, using sidelengths a, b, c instead of angles A, B, C, is
a (b^2 - c^2)(b^2 + c^2 - a^2) x + ... = 0.
This shortened notation enables an efficient list of lines perpendicular to the Euler line:
a x + ... = 0 (i.e., the line at infinity, with equation a x + b y + c z = 0)
(a^3) x + ... = 0
a(a + b)(a + c) x + ... = 0
(cos A) x + ... = 0
(sin 3A) x + ... = 0
(sin(A + pi/6)) x + ... = 0
(sin(A - pi/6)) x + ... = 0
a (cos^2 A) x + ... = 0
cos 2A cos(B - C) x + ... = 0
(sin 2A) cos(B - C) x + ... = 0.
Leonhard Euler
Schiffler point
Bailey point
Triangle Centers
Clark Kimberling Home Page