|
An isoscelizer for angle A in a triangle ABC is any line segment from a point P on side AC to a point Q on side AB such that the segments AP and AQ have equal lengths; i.e., triangle APQ is isosceles.
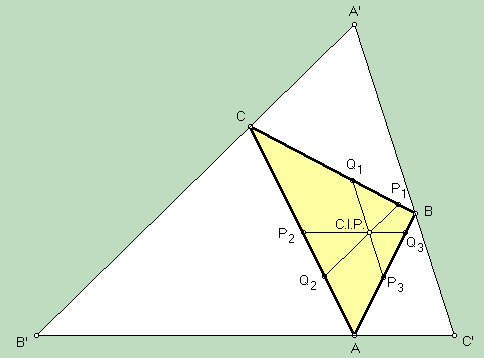
In 1989, Peter Yff (a Dutch name; just say ife) proved that there is a unique configuration in which the three angles A, B, C have isoscelizers of equal length, and that they meet in a point here named the congruent isoscelizers point. Yff also proved that trilinears for this point are
cos(B/2) + cos(C/2) - cos(A/2) :
|
|
The triangle A'B'C' shown in the figure is the excentral triangle. Several people were pleasantly surprised when a computer "discovered" that the Clawson point of A'B'C' is the congruent isoscelizers point.
(For a quick lesson on trilinears, click on TRILINEAR COORDINATES.)