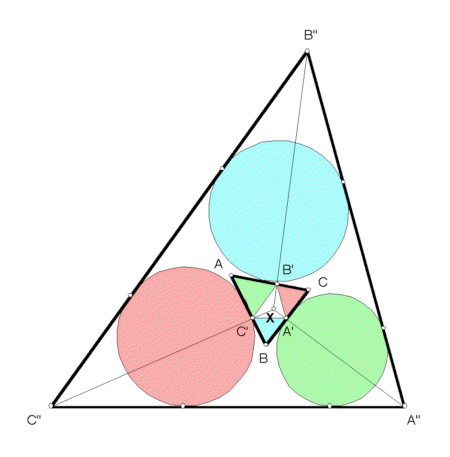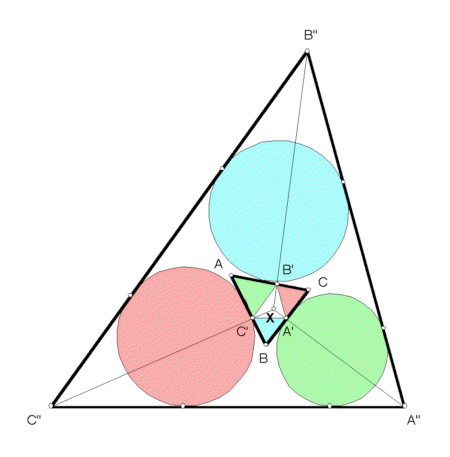CLAWSON POINT

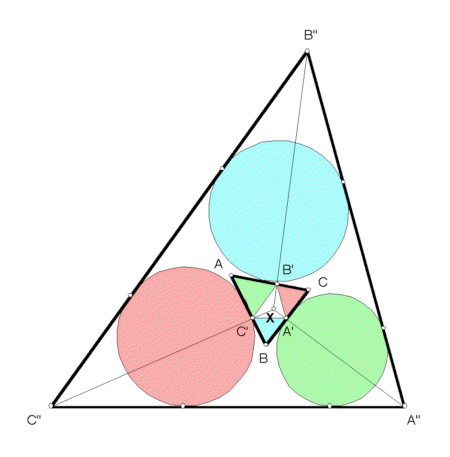
The Clawson point is the homothetic center of the orthic triangle and the extangents triangle. In the figure, the reference triangle is labeled ABC. Its orthic triangle, A'B'C', is formed by the feet of the altitudes of triangle ABC - for example, A' is the point in which the altitude through A meets side BC. The extangents triangle, labeled A"B"C", is formed by the lines externally tangent to the excircles of triangle ABC. The lines A'A", B'B", C'C" concur in the Clawson point, X, of triangle ABC.

Trilinear coordinates for the Clawson point are

tan A : tan B : tan C.

For a reference to Clawson's description of this point, by its trilinears, click on his name highlighted below. The construction given here first appears in

R. Lyness and G. R. Veldkamp, Problem 682 and Solution, Crux Mathematicorum 9 (1983) 23-24.

Initially, the point was thought to be new in 1983 and was called the crucial point after the journal in which it appeared.

(For a quick lesson on trilinears, click on TRILINEAR COORDINATES.)

To John Wentworth Clawson
To Triangle Centers (with access to a list of classical centers)
To Clark Kimberling Home Page