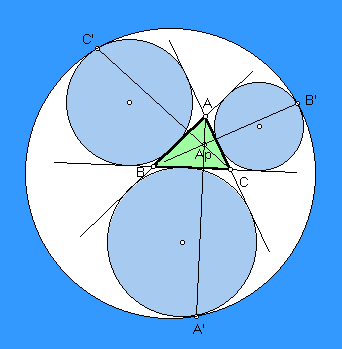
[sin(A) cos(B/2 - C/2)]^2 :
[sin(B) cos(C/2 - A/2)]^2 :
[sin(C) cos(A/2 - B/2)]^2.
|
Let Ea, Eb, Ec denote the excircles opposite A, B, C, respectively, in the plane of a triangle ABC. The famous problem of Apollonius includes the construction of the circle E that is internally tangent to the three excircles and encompassing them. Let A' be the point of tangency of circles Ea and E, and similarly for B' and C'. The lines AA', BB', CC' concur in the Apollonius point. Trilinear coordinates are
[sin(A) cos(B/2 - C/2)]^2 : |

|
The solution of the Apollonius problem has been known for centuries, but the Apollonius point may have been first noted in
C. Kimberling, Shiko Iwata, and Hidetosi Fukagawa, Problem 1091 and Solution,
Crux Mathematicorum 13 (1987) 128-129 [Proposed 1985]. See pages 217-218 also.