YFF-MALFATTI POINT

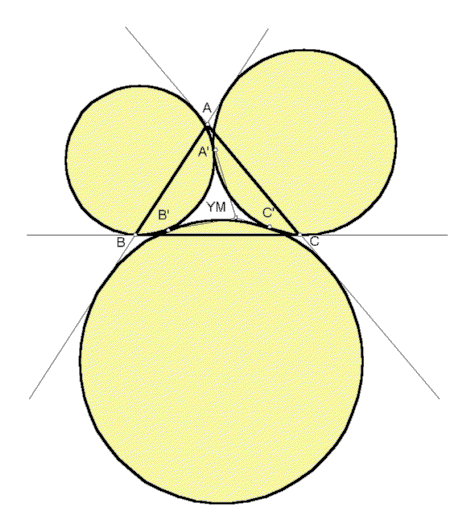
The Malfatti problem, dating from Ajima in the late 1700's and Malfatti in the early 1800's, is to construct three circles inside a triangle, each tangent to the other two and also tangent to two of the sidelines of the triangle. In 1997, Peter Yff considered the classical Ajima-Malfatti configuration and realized that if the requirement that the circles lie inside the triangle is dropped, then there is a second configuration that solves the problem.

Moreover, in analogy with the classical Ajima-Malfatti configuration, there is an interesting triangle center. In the figure, the reference triangle is labeled ABC, and the points of pairwise tangency of the circles are labeled A', B', C'. The lines AA', BB', CC' concur in the Yff-Malfatti point, labeled YM.

Trilinear coordinates for the Yff-Malfatti point are

[csc(A/4)]^4 : [csc(B/4)]^4 : [csc(C/4)]^4.

(For a quick lesson on trilinears, click on TRILINEAR COORDINATES.)

To Gian Francesco Malfatti
To Triangle Centers (with access to a list of classical centers)
To Clark Kimberling Home Page