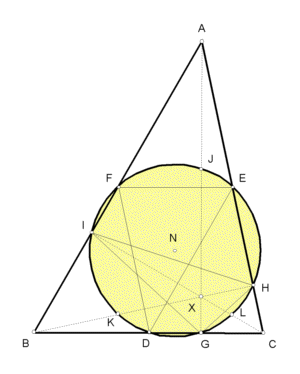
D = the midpoint of side BC,
E = the midpoint of side CA,
F = the midpoint of side AB;
G = foot on BC of altitude from A,
H = foot on CA of altitude from B,
I = foot on AB of altitude from C;
J = midpoint of segment AX,
K = midpoint of segment BX,
L = midpoint of segment CX.
(X, the orthocenter, is where the altitudes AG, BH, CI meet.)
As you see in the sketch, a circle passes through all nine of the points D,E,F,G,H,I,J,K,L. It is the nine-point circle of triangle ABC, and its center, N, is the nine-point center.