1 - cos(B - C):
1 - cos(C - A):
1 - cos(A - B).
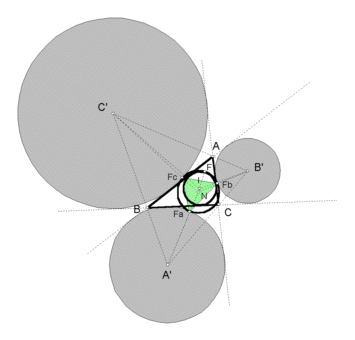
The points labeled Fa, Fb, Fc are the vertices of the Feuerbach Triangle. Although not shown in the figure, the lines A-to-Fa, B-to-Fb, C-to-Fc meet in the harmonic conjugate of F, having trilinears
1 + cos(B - C):
1 + cos(C - A):
1 + cos(A - B)
A discussion of the Feuerbach point and biography of K. W. Feuerbach (1800-1834) are given in
Dan Pedoe, Circles: A Mathematical View, Mathematical Association of America, Washington, D. C., 1995.