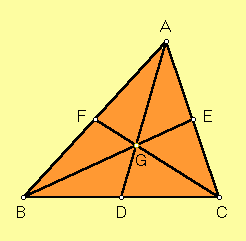|
In the plane of any triangle ABC, let
D = midpoint of side BC, As you see in the sketch, the lines AD, BE, CF all come together in one point, called the centroid of triangle ABC. There are many other points that are called triangle centers, but unlike most of them, "centroid" works on arbitrary shapes. |
|
|
For example, you can form the centroid (also called center of mass or center of gravity) of Texas.
Cut out a map of Texas from cardboard, hang it by a string, and draw a vertical line from the point of suspension down across the cardboard. Then remove the string, rotate Texas a few degrees, and repeat the procedure. Your two lines will meet right at the centroid. (It's not far from the capital, Austin.) One of the many interesting properties of the centroid of a triangle is that it is the unique point P for which the three triangles BCP, CAP, ABP all have the same area. |
|
