|
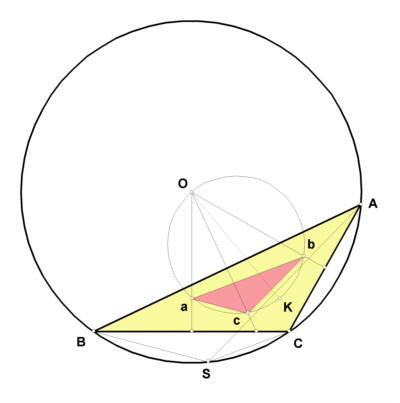
The Steiner point of a triangle ABC is constructed as follows: First, let O be the circumcenter and K the symmedian point of ABC. The circle having segment OK as diameter is the Brocard circle. The line through O perpendicular to line BC passes through the Brocard circle in another point, a; similarly, obtain points b and c. The triangle abc is the 1st Brocard triangle. Now, construct the line through A parallel to line bc, the line through B parallel to line ca, and the line through C parallel to line ab. These three lines concur in the Steiner point, S.
|

|
J. Neuberg, "Sur le point de Steiner," Journal de mathématiques spéciales 1886, p. 29,
the point was constructed as described here and was given Steiner's name.
Steiner also first described the ellipse passing through the vertices A, B, C and having the centroid of triangle ABC as its center. This Steiner ellipse is the ellipse of least area that passes through these points. It has in common with the circumcircle of ABC not only the points A, B, C but also the Steiner point.
Homogeneous trilinear for the Steiner point are
bc/(b^2 - c^2) : ca/(c^2 - a^2) : ab/(a^2 - b^2),
where a,b,c denote the sidelengths of sides BC, CA, AB of triangle ABC. You can see easily without a pencil that the Steiner point lies on the Steiner ellipse, which has equation
1/ax + 1/by + 1/cz = 0.