INCENTER

In the plane of any triangle ABC, let

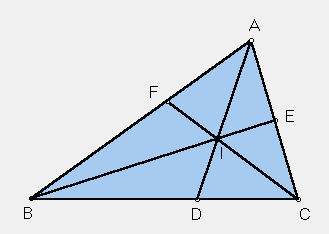
D = the point in which the bisector of angle A meets side BC,
E = the point in which the bisector of angle B meets side CA,
F = the point in which the bisector of angle C meets side AB.

As you see in the diagram, the three bisectors all come together in one point, called the incenter of triangle ABC. The incenter is equidistant from the three sidelines, and so the common distance is the radius of a circle that is tangent to the sidelines. It is called the incircle.

If you extend the sidelines of triangle ABC, then you can draw three more circles that are tangent to the sidelines. The centers of these circles are determined by bisectors of external angles at A, B, C. A picture is worth a hundred words - the internal bisectors are shown in blue, the externals in green.

The points A', B', C' are called the excenters. Trilinear coordinates for these and other points are

A = 1 : 0 : 0
B = 0 : 1 : 0
C = 0 : 0 : 1
I = 1 : 1 : 1
A' = -1 : 1 : 1
B' = 1 : -1 : 1
C' = 1 : 1 : -1.

Triangle Centers (with access to a list of classical centers)
Clark Kimberling Home Page