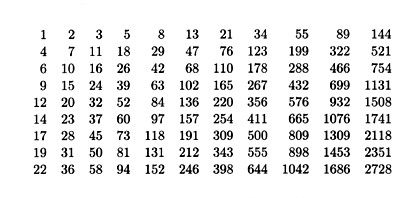
|
The numbers you see to the right form a northwest corner of the Wythoff array:
Interestingly, the Wythoff array (1) contains every positive integer exactly once, (2) has increasing rows and columns, and (3) has interspersed rows - i.e., once the first term of any row lies between two consecutive terms of any other row, the alternating between the two rows continues forever. The three properties define an interspersion. (The Wythoff array is only one of uncountably many interspersions.) |
|
Now, suppose X = ( x(1), x(2), x(3), . . . ) is an increasing sequence of positive integers, with x(1) > 1. Write 1,2,3,...,30 across the top of a piece of paper, and then beneath each of these n, write the number x(n). Then write out successive rows of an array as follows:
Row 1 consists of
1, x(1), x(x(1)), x(x(x(1))), . . .
Let i be the least positive integer not in row 1, and write row 2 as
i, x(i), x(x(i)), x(x(x(i))), . . .
Let j be the least positive integer not in row 1 or row 2, and write row 3 as
j, x(j), x(x(j)), x(x(x(j))), . . .
Continue indefinitely, obtaining a dispersion, namely that of the sequence x. In the article
C. Kimberling, "Interspersions and dispersions," Proceedings of the American Mathematical Society 117 (1993) 313-321,
it is proved that every interspersion is a dispersion, and conversely. Special cases are discussed in
N. J. A. Sloane, Classic Sequences in the Online Encyclopedia of Integer Sequences
A. Fraenkel and C. Kimberling, "Generalized Wythoff arrays, shuffles and interspersions," Discrete Mathematics 126 (1994) 137-149,
C. Kimberling, "Stolarsky interspersions," Ars Combinatoria 39 (1995) 129-138,
C. Kimberling, "The first column of an interspersion," Fibonacci Quarterly 32 (1994) 301-314.
C. Kimberling and J. Brown, "Partial complements and transposable dispersions", Journal of Integer Sequences 7 (2004) 147-159. Click here for a pdf file.
Interspersions are closely related to fractal sequences.