|
The continued fraction of the square root of 2 is
[1,2,2,2,2,2,2,2,2,2, . . .]. If you already know what this means, skip a few paragraphs. Otherwise, some introductory remarks are needed.
For any real number R, let [R] be the greatest integer less than or equal to R, and |
|
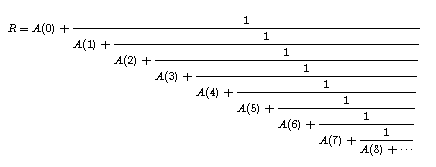
For example, [pi] = 3 and {pi} = .1416 (approx.). Now suppose R is irrational. Let A(0) = [R], and define inductively a sequence A(K) by A(K) = [F(K)], where
F(K+1) = 1/((F(K)-A(K))), for K = 0, 1, 2, . . . , and F(0) = R.
If you try this out on R = square root of 2, you'll find
A(0) = 1, A(1) = 2, A(2) = 2, A(3) = 2, A(4) = 2, A(5) = 2, and so on.
The sequence A(K) is written in the form [A(0), A(1), A(2), . . . ] and has been known for several hundred years as the continued fraction of R. The reason for the name is indicated by the pictured equation.
The continued fraction of R is studied largely through the behavior of a sequence of rational numbers called the convergents to R. To define convergents, begin with
P(-2) = 0, P(-1) = 1, P(I) = A(I)P(I - 1) + P(I - 2)
and
Q(-2) = 1, Q(-1) = 0, Q(I) = A(I) Q(I - 1) + Q(I - 2),
for I = 0, 1, 2, . . . . The convergents of R are the rational numbers P(I)/Q(I). The limit of the convergents is R. In fact, P(I)/Q(I) is called a best approximate to R, since it is closer to R than any rational number having smaller denominator than Q(I).
The bible of continued fractions - at least the old testament - is
Oskar Perron, Die Lehre von den Kettenbrüchen, Chelsea, New York, 1950.
Modern developments are given in many books, including
Claude Brezinski, History of Continued Fractions and Padé Approximants, Springer-Verlag, 1991.
One of the main applications of continued fractions is to best approximates of irrational numbers by rational numbers. However, if one asks for best lower approximates and best upper approximates, then the answers involve not only the convergents, but also intermediate convergents, as proved in
C. Kimberling, "Best lower and upper approximates to irrational numbers," Elemente der Mathematik, 52 (1997) 122-126.
The simplest infinite continued fraction is [1,1,1,1,1,1,1, . . .]. This equals (1 + (square root of 5))/2, a famous number called the golden mean. This number is closely related to the Fibonacci numbers (1, 1, 2, 3, 5, 8, 13, 21, 34, . . . ), since the convergents to the golden mean are ratios of Fibonacci numbers: 8/5, 13/8, 21/13, . . . .
There is a nice geometric way to describe the golden mean. A golden rectangle is a rectangle whose ratio of length to width is the golden mean. If you cut of the biggest square you can from an end of a golden rectangle, then the remaining rectangle is also golden. (So, if you continue cutting off the biggest remaining square, the resulting rectangle always has the same shape.) No other rectangle has this property.
However, you can start with any rectangle and, knowing the continued fraction for its length/width, you can tell how many maximal squares are available for each cutting - yes, for the Kth cutting, there will be A(K) maximal squares. See
C. Kimberling, "A visual Euclidean algorithm," Mathematics Teacher 76 (1983) 108-109.
Is there a "golden triangle"? Yes, in fact there are two, both described in the article
Clark Kimberling, "Two kinds of golden triangles, generalized to match continued fractions," Journal for Geometry and Graphics 11 (2007) 165-171.
One particularly interesting class of continued fractions [A(0), A(1), A(2), . . . ] are those for which all the partial quotients A(K) are less than some number. A survey of research on this class is
Jeffrey Shallit, "Real numbers with bounded partial quotients: a survey," L'Enseignement Mathématique 38 (1992) 151-187.
For given upper bound, the class can be ranked, as shown in
C. Kimberling, "A relative rank function on sets of continued fractions having bounded partial quotients," in Applications of Fibonacci Numbers, vol. 7, Kluwer Academic Publishers, Dordrecht (Netherlands), 1998, pages 201-213.
C. Kimberling, "Palindromic sequences from irrational numbers," The Fibonacci Quarterly 36 (1998) 171-173.