One of the best modern sources of information about Fibonacci is the following article:
ABSTRACT. The purpose of the article is to describe the contributions to Mathematics made by the thirteenth century Italian, Fibonacci. Unfortunately, not much is known about Fibonacci's personal life. Representative problems solved by Fibonacci are set as challenges to the reader.(1*)
[Asterisks refer to FOOTNOTES near the end of this article.]
"...considering both the originality and power of his methods, and the importance of his results, we are abundantly justified in ranking Leonardo of Pisa as the greatest genius in the field of number theory who appeared between the time of Diophantus [4th century A.D.] and that of Fermat" [17th century] R.B. McClenon [13].
[Numbers in square brackets refer to REFERENCES at the end of this article.]
THE MAN
1. The world of Fibonacci.
During the twelfth and thirteenth centuries, many far-reaching changes in the social, political and intellectual lives of people and nations were taking place. Europe had emerged from the period of barbarian invasions and disruption known as the Dark Ages. Improved techniques in farming had led to greater food production, population growth and commercial expansion which were to pave the way for the industrial, scientific and technological progress of later centuries. Contacts with Eastern civilizations were made by the Crusaders, by curious travellers and by merchants eager for trading opportunities.
By the end of the twelfth century, the struggle between the Papacy and the Holy Roman Empire had left many Italian cities independent republics. Having consolidated their military victories, many of these cities embarked on substantial trading enterprises, and some established centers for higher learning. In particular, ships from Genoa and Venice, laden with cargo for and from distant lands, helped to extend the maritime dominions of these cities which became the capitals of small empires.
Among these important and remarkable republics was the small but powerful walled city-state of Pisa which played a major role in the commercial revolution which was transforming Europe. A description of the many facets of the bustling life of medieval Pisa (which is thought to have had a population of about 10,000) may be found in Gies and Gies [4]. "Its citizens are brave", observed Benjamin of Tudela, a Spanish Jew, "and they have neither king nor prince to whom they owe obedience".
Into this world of change and cross-fertilisation of Christian and Moslem cultures, Fibonacci, a man for all seasons, was born in Pisa.
Pisa today is best known for its leaning tower (inclined at an angle of about 161/2o to the vertical). Unknown to most people is a statue in the Giardino Scotto erected by the citizens of Pisa to its most famous citizen, Fibonacci, the most outstanding Western mathematician of the Middle Ages and a man very much in advance of his time.
In this progressive and energetic city, Fibonacci was born in about 1175, i.e., about 800 years ago, though no one knows for certain the exact date of his birth. We take this opportunity to publicise the man and his contributions to Mathematics.
2. The young Fibonacci.
Fibonacci's father is mentioned by name by a contemporary writer as Gulielmus (William). Not much is known about the father except that he was a state official associated with the new mercantile class which had emerged from the commercial revolution.
No portraits of Fibonacci exist. Possibly, the imaginative description of the education, clothes and housing of people of medieval Pisa, as given in [4], was applicable to Fibonacci.
All that we do know about Fibonacci is contained in a few sentences about himself in the 1228 edition of his famous Liber Abbaci (sometimes spelt Liber Abaci). The translation of these passages, along with the original Latin, is given by Grimm [5] as follows:
After my father's appointment by his homeland as state official in the customs house of Bugia for the Pisan merchants who thronged to it, he took charge; and in view of its future usefulness and convenience, had me in my boyhood come to him and there wanted me to devote myself to and be instructed in the study of calculation for some days. There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily, and Provence, with their varying methods; and at these places thereafter, while on business. I pursued my study in depth and learned the give-and-take of disputation. But all this even, and the algorism, as well as the art of Pythagoras I considered as almost a mistake in respect to the method of the Hindus. Therefore, embracing more stringently that method of the Hindus, and taking stricter pains in its study, while adding certain things from my own understanding and inserting also certain things from the niceties of Euclid's geometric art. I have striven to compose this book in its entirety as understandably as I could, dividing it into fifteen chapters. Almost everything which I have introduced I have displayed with exact proof, in order that those further seeking this knowledge, with its pre-eminent method, might be instructed, and further, in order that the Latin people might not be discovered to be without it, as they have been up to now. If I have perchance omitted anything more or less proper or necessary, I beg indulgence, since there is no one who is blameless and utterly provident in all things.
(The port of Bugia (modern Bougie in Algeria) was a thriving source of raw materials for furs and leather, two of Pisa's industries.)
From this tantalizingly brief glimpse of Fibonacci's life, we gain some insight into his personality and the mathematical quality of his mind. Quite apart from the intellectual curiosity and excitement which these passages reveal, they leave us with a respect and warmth of feeling for the modest humility of the man. "Leonardo's humility graces his genius", says Grimm [5].
3. Fibonacci and the Emperor Frederick II.
Fibonacci's fame as a mathematician was so great that he attracted the attention of the Holy Emperor, Frederick II, whom his contemporaries called Stuper Mundi ("Wonder of the World"). Frederick was also King of the Two Sicilies and as such "kept a picturesque Arabian Nights court at Palermo, enlivened by dancing girls, jugglers, musicians, eunuchs, and an exotic menagerie", according to Gies and Gies [4].
At Frederick's Sicilian headquarters there was an intermingling of races and cultures. The Emperor, one of the most remarkable men of the Middle Ages, encouraged learning and scholarship of every kind, having a special interest in Mathematics and Science. We are told that Frederick himself conducted scientific experiments with incubating ovens to study the development of a chicken embryo and that he sealed the eyes of the vultures to determine whether they found their food by sight or smell. Furthermore, he wrote a book on falconry which contained valuable information on birds.
Fibonacci corresponded with two of the Emperor's scholars, Master Theodore and Michael Scott (whom Dante, in his Divina Commedia, consigned to hell as a wizard for perpetuating "magical frauds").
A meeting was arranged between Fibonacci and Frederick at the Emperor's palazzo in Pisa, Frederick bringing with him an imposing retinue of people and animals. Frederick, who was about 30 years old, is described [4] as "athletic-looking and of medium height, with reddish-blond hair and piercing blue eyes which are said to have made his courtiers tremble".
Mathematical questions for Fibonacci to solve were proposed by a scholar, Master John of Palermo. According to some writers, a mathematical tournament between Fibonacci and other mathematicians took place, but this does not seem to have been the case.(2*) Three of these problems are given later (§§7, 8) when I deal with Fibonacci's mathematical writings. At the time of his meeting with Frederick in the 1220's, Fibonacci was probably at the height of his prowess.
4. The last years.
The last we hear of Fibonacci is in a document issued by the commune of Pisa in 1240. This granted an annual honorarium of 20 Pisan pounds, plus expenses, for community services to "the discreet and learned man, Master Leonardo" [4].
No one knows when Fibonacci died nor under what circumstances his death occurred. Within a few decades of his death, Pisa was disastrously defeated by Genoa in the grim naval battle of Meloria and the decline of his native city had irreversibly begun. The proud inscription on Pisa's "golden" sea gate,
"Love justice, ye rulers of the earth!"
became a nostalgic memory of past grandeur.
What did Fibonacci look like? Did Fibonacci marry? Did he have any children? What was the state of his health? his wealth? What were his political views? To what extent, if at all, did he rely on the works of the Greeks (e.g. the (now) lost books of Diophantus)? It is a great pity indeed that we do not know more about this remarkable man.
THE MATHEMATICIAN
5. Fibonacci's works.
The mathematical writings of Fibonacci known to us and their dates are [2]:
Liber Abbaci (The Book of Calculation), 1202 (1228);
Practica Geometriae (The Practice of Geometry), 1220;
Liber Quadratorum (The Book of Square Numbers), 1225;
Flos (The Flower), 1225;
Letter to Master Theodore (cf. §3).
In my discussion of his works, I shall endeavour to show some of the types of mathematical problems Fibonacci solved, and to indicate something of the originality and ingenuity of his approach. From time to time, I shall propose some of Fibonacci's simpler problems as challenges to the reader. Answers to these problems (with comments) will be published in a later issue of The Australian Mathematics Teacher. Thus, I allow myself the luxury of vicariously playing the role of John of Palermo to the reader's Fibonacci! Many of these problems are chosen so as to be within the grasp of interested high school students.
6(a). Liber Abbaci: Hindu-Arabic numerals.
In 1202, Fibonacci's hand-written account, Liber Abbaci, of his new mathematical experiences arising from the contacts he made on his Mediterranean travels was completed in Pisa. Unfortunately there doesn't appear to be any trace of this original version. The monumental revised edition, dedicated (3*) to Michael Scott (§3), was compiled by Fibonacci in 1228, and this is the one we know.(4*) "Its publication", say Gies and Gies [4], "was a landmark in both the history of the Middle Ages and the history of mathematics".
Though the title of the book suggests the use of the abacus, in fact Fibonacci freed arithmetic from calculations using the abacus. He did this by introducing to Western Europe in a clear, comprehensive and independent way, the new Hindu-Arabic numerals which had been successfully used in the Middle East and the Orient. McClenon [13] states that the Liber Abbaci was the "greatest arithmetic of the middle ages and the first one to show by examples from every field the great superiority of the Hindu-Arabic numeral system over the Roman system exemplified by Boethius" (the arithmetic most generally taught throughout Europe before the thirteenth century).
It was not, however, the first book written in Europe to use and explain the new numerals, nor did it achieve the popularity of later, more elementary descriptions such as that of the thirteenth century English schoolman, Sacrobosco (John of Halifax).
Fibonacci's Liber Abbaci begins (page 2 of [2]) with the simplest but profound statement:
The nine Indian figures are :
9 8 7 6 5 4 3 2 1
With these nine figures, and with the sign 0 ... any number may be written, as is demonstrated below.
With regard to the symbol 0 "which in Arabic is called zephirum" (quod arabice zephirum appellatur [2]), we note that the words cipher and zero come from the Arabic.
In the Liber Abbaci, Fibonacci explains (sometimes tediously) the nature of the Hindu-Arabic numerals, their use in calculations with integers and fractions, and their applications to practical commercial problems relating to weights and measures, bartering, interest and money-changing. In the remainder of his book, Fibonacci is more concerned with theoretical, rather than practical, problems, e.g. Series and Proportions, the Extraction of Square and Cube Roots, the use of the Rule of False Position, the Method of Casting out Nines (for checking calculations), and other techniques discovered by the Hindu and Arab mathematicians. Finally, he deals with geometry and algebra. For ease in calculation with the new numerals, Fibonacci provides tables for the four arithmetical operations.
Recall that the symbols "+" and "-" were not invented until the fifteenth century while "÷" appeared in the seventeenth century. Following precedent and necessity, Fibonacci writes out these operations in words or else illustrates his calculations with diagrams. There being no algebraic symbolism available to him, Fibonacci uses res (thing) for the unknown x, and for x2 he writes quadratus numerus (square number).
While discussing the merits of the new system of numeration, Fibonacci also makes reference to the then current Roman numerals for comparison, and to the sexagesimal system of the Babylonians. Not everyone, however, accepted the usefulness of these Oriental symbols. For example, in 1299, Florentine merchants issued an ordinance prohibiting the use of Hindu-Arabic numerals because it was too easy for an unscrupulous person to write a sum of money, say 1000 lire, as 1999 lire. Such a fraudulent alteration was impossible in Roman numerals.
To give something of the flavour of Fibonacci's work we quote [4] the following theoretical and commercial problems:
PROBLEM 1 (The Lion and the Pit: De leone quite erat in puteo). A pit was 50 handbreadths in depth: A lion climbed up the pit 1/7 handbreadth every day and fell back 1/9 handbreadth. How long would it take him to get out of the pit?
(We recognize this as a variant of the familiar Frog-in-the-Well brain teaser. Problem 1 and Problem 2 (below) occur on pages 177 and 398 respectively of [2].)
PROBLEM 2 (Birds and Towers). Two birds start flying from the tops of two towers 50 feet apart, one 30 feet high, the other 40 feet high, starting at the same time and tat the same rate. They reach the center of a fountain between the towers at the same time. How far is the fountain from each tower?
PROBLEM 3 (A Voyage). A certain man doing business in Lucca doubled his money there, and then spent 12 denarii. Thereupon, leaving he went to Florence; there he also doubled his money, and spent 12 denarii. Returning to Pisa, he there doubled his money and spent 12 denarii, nothing remaining. How much did he have in the beginning?
PROBLEM 4 (An Inheritance). A man whose end was approaching summoned his sons and said: "Divide my money as I shall prescribe." To his eldest son, he said, "You are to have 1 bezant and a seventh of what is left." To his second son he said, "Take 2 bezants and a seventh of what remains." To the third son, "You are to take 3 bezants and a seventh of what is left." Thus he gave each son 1 bezant more than the previous son and a seventh of what remained, and to the last son all that was left. After following their father's instructions with care, the sons found that they had shared their inheritance equally. How many sons were there, and how large was the estate?
For further problems from Liber Abbaci, see[4], Appendix 1.
A hardy perennial recreational problem occurring in Fibonacci's book, which may have been suggested by a similar problem in the ancient Egyptian Rhind papyrus (written by the scribe Ahmes) tells us that:
seven old women went to Rome; each woman had seven mules; each mule carried seven sacks; each sack contained seven loaves; and with each loaf were seven knives; each knife was put in seven sheaths.
(This is reminiscent of the childhood jingle: "As I was going to St. Ives, I met a man with seven wives, . . . ".)
6(b). Liber Abbaci: number theory.
Besides the emphasis on the Hindu-Arabic numerals, Fibonacci's other main contribution in the Liber Abbaci was in number theory.
A third type of problem, familiar to many mathematicians and associated with the Chinese, is the remainder problem. Fibonacci asks, and correctly answers, these problems:
PROBLEM 5 (Remainder Problems).
(i) Find a number which is divisible by 7 and which gives a remainder of 1 when divided by 2, 3, 4, 5, or 6.
(ii) Find a number which is a multiple of 7 having remainders of 1, 2, 3, 4 and 5 when
divided by 2, 3, 4, 5 and 6.
6(c). Liber Abbaci: the Fibonacci sequence.
In Chapter 12 of the Liber Abbaci (pages 283-4 of [2]), Fibonacci states the problem which involves the famous sequence with which his name is irrevocably linked (Quot paria coniculorum in uno anno ex uno paro germinentur):
A certain man put a pair of rabbits in a place surrounded by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?
Since Fibonacci's time his sequence (which was not important to him) has generated nearly as many research papers as it has hypothetical rabbits! For the history of the work on the sequence until about 1920 we might consult Dickson [1]. Since the foundation of the Fibonacci Association in San José, California, in the 1960's, and the production of the Fibonacci Quarterly (a journal devoted to the study in integers with special properties) there has been an orgy of creativity in which this author has shamelessly participated.
It is not my intention to detail properties of the Fibonacci numbers and of the related Lucas numbers which are well-documented elsewhere. For readable information on these fascinating aspects of Mathematics, see Hoggatt [7], Jarden [11], Lucas [12] and Vorobev [15]. Readily accessible material on the Fibonacci numbers may be found in past issues of The Australian Mathematics Teacher in articles by Guest [6], Horadam [8]-[10] and MacDonald [14].
Current research in modern extensions of Fibonacci's ideas is to be found in issues of the Fibonacci Quarterly [3] which began in 1963.
7. Liber Quadratorum.
Dedicated to Frederick II (§3), this brilliant book was written by Fibonacci after his Liber Abbaci. In it, Fibonacci shows his mathematical prowess in solving Diophantine problems (named after Diophantus, the fourth century A.D.Greek scholar who lived in Alexandria). His problems involve second degree equations in two or more unknowns, the solutions for which are required to be given as integers or rational numbers. Such problems are not easy, particularly when one wishes to generalise solutions and when the algebraic symbolism Fibonacci needed was not at his disposal.
It has been stated [4] that
The Liber Quadratorum, a book with less immediate influence and narrower scope than the Liber abaci, was nevertheless an even greater masterpiece, more original and involving subtler reasoning, a systematically arranged, well-conceived collection of theorems many of them written by Leonard [Fibonacci], others discovered from Indian or Arabic sources, but using proofs which were the product of Leonard's own ingenuity.
McClenon [13] says:
The usual method of proof employed is to reason upon general numbers which Leonardo represents by line segments. He has . . . no algebraic symbolism, so that each result of a new operation (unless it be a simple addition or subtraction) has to be represented by a new line. But for one who had studied the 'geometric algbra' of the Greeks, as Leonardo had, in the form in which the Arabs used it, this method offered some of the advantages of our symbolism; and at any rate it is marvelous with what ease Leonardo keeps in his mind the relation between two lines and with what skill he chooses the right road to bring him to the goal he is seeking.
Fibonacci obtains results which are equivalent to:
It is claimed [13] (5*) that this last result should be called "Leonardo's Theorem" as it was not definitely stated in any earlier work. Results (ii) and (iii) are attributed by Proclus to Pythagoras and Plato respectively.
Fibonacci was stimulated to compile his Liber Quadratorum by consideration of one of the problems proposed to him by John of Palermo (§3):
PROBLEM 6. Find a square number which, being increased or diminished by 5, gives a square number.
An extension of PROBLEM 6 is:
Find a number which, being added to, or subtracted from, a square number, leaves in either case a square number.
McClenon [13] remarks that Fibonacci's proof of this is "so very ingenious and original" but long and that "It is not too much to say that this is the finest piece of reasoning in number theory of which we have any record, before the time of Fermat".
The following problems of Fibonacci are left to the reader (see [13] for others):
PROBLEM 7. Find a number of the form 4xy(x + y)(x - y) which is divisible by 5, the quotient being a square. (Fibonacci calls a number of this form a congruum.)
PROBLEM 8. Solve in rational numbers the pair of equations
x2 + x = u2, x2 - x = v2.
The Liber Quadratorum concludes with the problem of solving in rational numbers the equations
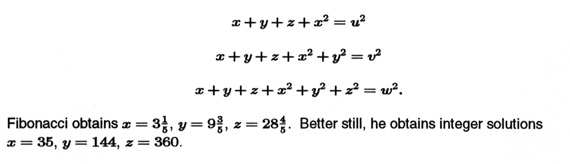
Fibonacci obtains x = 3 1/5, y = 9 3/5, z = 28 4/5. Better still, he obtains integer solutions x = 35, y = 144, z = 360.
Fibonacci goes on to say [13]:
And not only can three numbers be found in many ways by this method but also four can be found by means of four square numbers, two of which in order, or three, or all four added together make a square number . . . I found these four numbers, the first of which is 1295, the second 4566 6/7, the third 11417 1/2, and the fourth 79920.
The MS of Liber Quadratorum ceases fairly abruptly at this point. The rest is silence.
8. Flos (The Flower).
In this short work (the title of which might suggest that algebra is the "flower of Mathematics"), Fibonacci describes inter alia two of the Diophantine problems he worked on at the court of the Emperor Frederick (§3). These are, in our phrasing:
PROBLEM 9. Solve x3 + 2x2 + 10x = 20.
(Fibonacci recognises that Euclid's method of solving equations by square roots would not work and devises an original method of his own, giving his answer in (Babylonian) sexagesimal notation. His approximation was far more accurate than those of his Arab contemporaries.)
PROBLEM 10. Three men owned some money, their shares being 1/2, 1/3, and 1/6. Each took some money at random until none was left. The first man then returned 1/2 of what he had taken, the second 1/3 and the third 1/6. When the money now in the pile was divided equally among the men, each possessed what he was entitled to. How much money was in the original store, and how much did each man take?
9. Practica Geometriae (The Practice of Geometry).
This substantial, well-written book (with its rigorous proofs) contains several chapters of mainly Euclidean theorems which represent "a considerable advance over the Geometry of Boethius and Gerbert (Pope Sylvester II)" [4].
It is worth noting that, in 1915, R. C. Archibald based his Euclid's Book on Division of Figures (a restoration of Euclid's lost work) on Woepeke's French translation of an Arabian MS, and on Fibonacci's Practica Geometriae.
THE IMPORTANCE OF FIBONACCI
From Fibonacci's commercial problems we can learn much about the society in which he lived. For instance, the sociologist and economist can discover that pepper was a very important item of merchandise transported by Pisan ships, and that the Pisan colony in Constantinople traded extensively with Egypt. Further evidence is also gleaned about the relative values of money coined in the mints of different cities, and about the problem of alloying of coins to be minted.
After Fibonacci's death, his influence languished for many centuries and indeed Mathematics made no real progress for 300 years.
What is the legacy we have inherited from Fibonacci?
Hindu-Arabic numerals were obviously relevant to the expanding commerce-oriented society of his day. Of greater importance was the long-range impact on Science and Mathematics of the new system of numeration which he publicised.
The quality of his mind is evident in the techniques he used to demolish the more challenging problems he encountered. Yet few latter-day mathematicians recognised his brilliance, possibly because of the forbidding barrier placed in their way by his untranslated Latin, coupled with his relative obscurity.
Apart from the statue to his memory in the Giardino Scotto [it was formerly there; see above for the present location], Fibonacci's name is perpetuated in two streets, the quayside Lungarno Fibonacci in Pisa and the Via Fibonacci in Florence. Few people know of these minor memorials.
Strangely, Fibonacci is best remembered by the sequence which bears his name but which, ironically, he treated only lightly. Modern mathematicians, in naming an Association, a Journal, and a Bibliographical and Research Centre after Fibonacci, ensure that his name will not easily be forgotten.
Some recent research publications which owe their original stimulation to Fibonacci's sequence are:
Carlitz, L., "Reduction Formulas for Fibonacci Summations", Fibonacci Quarterly Vol. 9, No. 5, Dec. 1971, pp. 449-467;
Hoggatt, V. E., "Generalized Zeckendorf Theorem", Fibonacci Quarterly, Vol. 10, No. 1, Jan. 1972, pp. 89-93;
Shannon, A. G., and Horadam, A. F., "Generating Functions for Powers of Third Order
Recurrence Sequences", Duke Mathematical Journall, Vol. 38, No. 4, Dec. 1971,
pp. 791-794;
Subba Rao, K., "Some Properties of Fibonacci Numbers - I", Bulletin of Calcutta
Mathematical Society, Vol. 46, No. 4, 1954, pp. 253-257.
As has been truly said [4] of Fibonacci, he is "one of the world's great intellectual pioneers". Further, Boyer, in A History of Mathematics, appropriately assesses Fibonacci's capability in these words: "It is true that he was without a worthy rival during the 900 years of medieval European culture".
A generation wiser than his own (or ours) with a deeper sense of enduring values may have been bestowed on him the accolade: Stupor Mundi.
FOOTNOTES
(1) The subject of our article is known variously as Leonard(o) of Pisa, Leonardus Pisanus, Pisano, Leonard Fibonacci, or, more widely, Fibonacci. It is this last name which we will use. Fibonacci is thought to be a contraction of Filiorm Bonacci ("of the family of Bonacci") or Filius Bonacci ("son of Bonacci"). [He is not to be confused with that other famous Leonardo, the universal genius from Vinci.] Another name by which Fibonacci is known is Leonardus Bigolius, "bigollo" being a Tuscan dialect word roughly translatable as "absent-minded" [4].
(2) Public problem-solving mathematical contests have been known. One such "tournament" occurred in 1535 between Antonio Maria Fior from Venice and Niccolo Tartaglia from Brescia, which was won easily by Tartaglia.
(3) Preceding the dedication is the Latin introductory heading: Incipit liber Abaci Compositus a leonardo filio Bonacij Pisano In Anno, M0 cc0 ij0 .
(4) This 1228 edition (the only complete printed edition) is one printed by Baldassarre Boncompagni [2] in Rome in the period 1857-1862. While Boncompagni knew of the existence of six manuscripts containing Fibonacci's autobiography, he based his edition on only one manuscript, "the handsome but frequently badly faded Coventi Soppressi C.I. 2616, dated to the early fourteenth century" [5]. This manuscript is now located in the Biblioteca Nazionale Centrale in Florence. Translation of Fibonacci's "spare Latinity" is made difficult by slight variations in the 6 manuscripts (which Grimm in his translation collated) and by the fact that Fibonacci wrote 13th century Tuscan Latin.
In a recent communication to me, Professor Grimm comments: "The best MS is in Siena and it is from this one (and it may be the oldest) that a new text should start." Because of the great complications involved in a scholarly translation of Liber Abbaci, it will be some years before an English version of Fibonacci's work can be expected.
(5) This claim is also made on p.233 of Gino Loria's Storia delle Matematiche, 1950. However, Carl Boyer, on p.283 of A History of Mathematics, 1968, asserts that these identities "had appeared in Diophantus and had been widely used by the Arabs. Fibonacci, in some of his problems and methods, seems to follow the Arabs closely". In Book III Problem 19 of his Arithmetica ("To find four numbers such that the square of their sum plus or minus any one singly gives a square"), Diophantus does assume a knowledge of these identities in the special case he deals with. See the comments on pages 105-106 in T. L. Heath's Diophantus of Alexandria, 1964. Fibonacci appears to have been generally influenced by the Arab mathematicians, al-Karkhi and al-Khowarizmi, who in turn were influenced by Diophantus.
REFERENCES
[1] Dickson, L. E., History of the Theory of Numbers, Vol. 1, 1952, pp. 393-407.
[2] Fibonacci, Scritti di Leonardo Pisano (ed. Baldassarre Boncompagni, 1857-1862).
[3] Fibonacci Quarterly, 1963-.
[4] Gies, Joseph and Gies, Frances, Leonard of Pisa and the New Mathematics of the Middle Ages, Thomas Y. Crowell, 1969.
[5] Grimm, R. E., "The Autobiography of Leonardo Pisano", Fibonacci Quarterly, Vol. 11, No. 1, February 1973, pp. 99-104.
[6] Guest, J., "A Variant to Fibonacci's Sequence", A.M.T., Vol. 16, No. 1, 1960, pp. 11-15.
[7] Hoggatt, V. E., Fibonacci and Lucas Numbers, Houghton Mifflin, 1969.
[8] Horadam, A. F., "Pythagorean Numbers and Fibonacci Sequences", A.M.T., Vol. 17, No. 2, July 1961, pp. 32-35.
[9] Horadam, A. F., "Fibonacci and his wonderful numbers", A.M.T., Vol. 19, No. 3, November 1963, pp. 54-60.
[10] Horadam, A. F., "Individual Study for Forms V and VI - Fibonacci Numbers", A.M.T., Vol. 22, No. 2, July 1966, p. 44.
[11] Jarden, D., "Recurring Sequences", Riveon Lematematika, Jerusalem, 1966.
[12] Lucas, E., Theorie des Nombres, Blanchard, 1961.
[13] McClenon, R. B., "Leonardo of Pisa and his Liber Quadratorum", American Mathematical Monthly, Vol. 26, No. 1, January 1919, pp. 1-8.
[14] MacDonald, T. H., "Deriving Properties of the Fibonacci Sequence", A.M.T., Vol. 29, No. 4, 1973, pp. 235-238.
[15] Vorob'ev, N. N., Fibonacci Numbers, Pergamon. 1961.
Fibonacci Numbers and the Golden Section (Ron Knott, U. of Surrey)
Fibonacci Number-Theorists
Clark Kimberling Home Page
